偏態分布是與“常態分配”相對,分布曲線左右不對稱的數據次數分布,是連續隨機變數機率分布的一種。可以通過峰度和偏度的計算,衡量偏態的程度。可分為正偏態和負偏態,前者曲線右側偏長,左側偏短;後者曲線左側偏長,右側偏短。
基本介紹
- 中文名:偏態分布
- 外文名:skewed distribution
- 特點:左右不對稱
- 類型:正偏態分布和負偏態分布
- 領域:統計學
- 別名:非對稱分布、歪分布
定義
種類
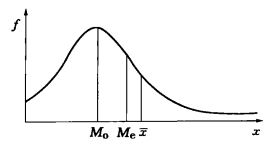 圖1(a) 正偏態
圖1(a) 正偏態 圖1(b) 負偏態
圖1(b) 負偏態分組下的眾數





偏離係數










偏態分布是與“常態分配”相對,分布曲線左右不對稱的數據次數分布,是連續隨機變數機率分布的一種。可以通過峰度和偏度的計算,衡量偏態的程度。可分為正偏態和負偏態,前者曲線右側偏長,左側偏短;後者曲線左側偏長,右側偏短。
 圖1(a) 正偏態
圖1(a) 正偏態 圖1(b) 負偏態
圖1(b) 負偏態














偏態分布是與“常態分配”相對,分布曲線左右不對稱的數據次數分布,是連續隨機變數機率分布的一種。可以通過峰度和偏度的計算,衡量偏態的程度。可分為正偏態和負...
正偏態(positive skewness)分布不對稱為偏態。分布高峰偏左,長尾向右延伸的偏態分布稱為正偏態,亦稱右偏態。此時均數大於眾數。...
偏態(skewness)是指非對稱分布的偏斜狀態。換句話說,就是指統計總體當中的變數值分別落在眾數(M0)的左右兩邊,呈非對稱性分布。偏態於1895年由統計學家皮爾遜(K...
負偏態(negative skewness)亦稱“左偏態”,指在一個不對稱或偏斜的次數分布中,次數分布的高峰偏右,而長尾則從右逐漸延伸於左端。即次數分布的眾數是在較大分數...
非正態分布(abnormal distribution)在通常的情況下,觀測試驗數據遵從正態分布,可用觀測值的平均值和標準差分別描述它的集中趨勢和離散特性。...
成績正態分布,一種機率分布的特殊表現形式,在統計某次考試成績分布規律的時候,將成績按分數段製成如右圖類似的統計圖,如果成績分布如右圖所示,中等成績占最多數,...
偏態係數又稱偏差係數,說明隨機系列分配不對稱程度的統計參數,用Cs表示。和Cv只能反映頻率密度分配曲線的平均情況和離散程度,而不能反映其對稱(即偏態)情況,所以...
在日常生活和經濟管理中,常見的頻數分布曲線主要有鐘形分布(常態分配、偏態分布)、J形分布、U形分布,洛倫茨分布曲線等幾種類型。...
偏斜度是對統計數據分布偏斜方向及程度的度量。統計數據的頻數分布有的是對稱的,有的是不對稱的,即呈現偏態。在偏態分布中,當偏斜度為正值時,分布正偏,即眾數...
1°數據分布最多,最集中(眾數組)和最少的小組;2°數據分布(頻數)的變化趨勢與分布狀態;3°中位數和平均數在哪個小組,是否是偏態分布;...
3、難度水平的確定要考慮對分數分布的影響,一般以正偏態分布為前提,有時正偏態分布更能激發學生的學習積極性。試題難度係數分類 編輯 預估試題難度係數:考試前通過...
