負偏態(negative skewness)亦稱“左偏態”,指在一個不對稱或偏斜的次數分布中,次數分布的高峰偏右,而長尾則從右逐漸延伸於左端。即次數分布的眾數是在較大分數或量數的一側(右側),而長尾是在較小分數或量數的一側(左側)。這種分布的偏態係數小於零。
基本介紹
- 中文名:負偏態
- 外文名:negative skewness
- 別稱:左偏態
- 特點:偏態係數小於零,分布的高峰偏右
- 所屬學科:數學(統計學)
- 相關概念:偏態分布,眾數,常態分配等
定義
圖像及參數分析





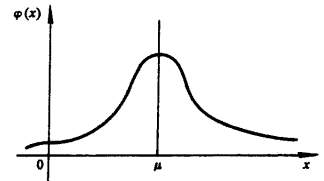 圖1
圖1






 圖2
圖2















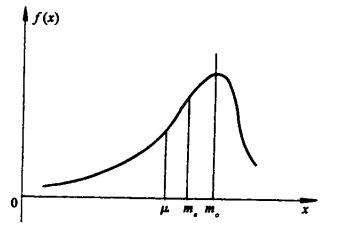 圖3
圖3



負偏態(negative skewness)亦稱“左偏態”,指在一個不對稱或偏斜的次數分布中,次數分布的高峰偏右,而長尾則從右逐漸延伸於左端。即次數分布的眾數是在較大分數或量數的一側(右側),而長尾是在較小分數或量數的一側(左側)。這種分布的偏態係數小於零。





 圖1
圖1






 圖2
圖2















 圖3
圖3


負偏態(negative skewness)亦稱“左偏態”,指在一個不對稱或偏斜的次數分布中,次數分布的高峰偏右,而長尾則從右逐漸延伸於左端。即次數分布的眾數是在較大分數...
偏態分布是與“常態分配”相對,分布曲線左右不對稱的數據次數分布,是連續隨機變數機率分布的一種。可以通過峰度和偏度的計算,衡量偏態的程度。可分為正偏態和負...
偏態(skewness)是指非對稱分布的偏斜狀態。換句話說,就是指統計總體當中的變數值分別落在眾數(M0)的左右兩邊,呈非對稱性分布。偏態於1895年由統計學家皮爾遜(K...
正偏態(positive skewness)亦稱“右偏態”。指在一個不對稱或偏斜的次數分布中,次數分布的高峰偏左,而長尾則從左側逐漸延伸於右端。即次數分布的眾數在較小分數...
偏態係數又稱偏差係數,說明隨機系列分配不對稱程度的統計參數,用Cs表示。和Cv只能反映頻率密度分配曲線的平均情況和離散程度,而不能反映其對稱(即偏態)情況,所以...
當多數數據集中在曲線的一端,而少數數據在曲線的另一端,數據分布的形態就產生了偏斜。當偏斜的一邊的趨向正數的方向,叫正偏態。當偏斜的一邊的趨向負數的方向叫...
寬厚誤差亦稱寬鬆誤差(Leniency),即評定結果是負偏態分布,也就是大多數員工被評為優良。...
寬厚錯誤亦稱寬厚誤差(Leniency),是指在績效考核中將大多數員工評為優良,即評定結果是負偏態分布。與其相對應的概念是嚴苛偏差。...
中心動差是指各單位變數值與平均數離差K次方的平均數,也稱為中心矩。中心矩偏態係數是用三階中心動差除以標準差的三次方對比得到,用α3表示。當α3=0時,...
證券出借業務的回報展示了典型的負偏態分布(negatively skewed distribution)的形態,以及不具吸引力的投資屬性。如同其他形式的出借業務一樣,證券出借的獲利空間僅限於...
在正偏態分布中M>Md>Mo在負偏態分布中M<Md<Mo三者關係 M即平均數,Md即中數,Mo即眾數詞條圖冊 更多圖冊 參考資料 1. [1]張厚粲, 徐建平. 現代心理與教育...
偏度(skewness)也稱為偏態、偏態係數,是統計數據分布偏斜方向和程度的度量,是統計數據分布非對稱程度的數字特徵。...
為X的偏度係數。偏度係數用以描述正態分布的分布形狀特徵。測度地理數據分布的不對稱性情況,刻畫以平均值為中心的偏向情況, g1<0,表示負偏,即均值在峰值的左邊;...
偏斜度是對統計數據分布偏斜方向及程度的度量。統計數據的頻數分布有的是對稱的,有的是不對稱的,即呈現偏態。在偏態分布中,當偏斜度為正值時,分布正偏,即眾數...
表示變數機率分布對稱性和分布方向的相對指標,也稱偏態係數,代表符號為Cs。...... 分布呈正偏態,Sk<0時,分布呈負偏態,Ku>3時曲線比較陡峭,Ku<3時曲線比較平坦...
偏態分布是指頻數分布不對稱,集中位置偏向一側,若集中位置偏向數值小的一側,稱為正偏態分布;集中位置偏向數值大的一側,稱為負偏態分布,如冠心病、大多數惡性腫瘤...
