定義
簡介
1.頻數表(frequency table)的編制
在觀察值個數較多時,為了解一組同質觀察值的分布規律和便於指標的計算,可編制
頻數分布表,簡稱頻數表。
(1)求全距(range):找出觀察值中的最大值與最小值,其差值即為全距(或
極差),用R表示。
(2)確定組段和
組距:根據樣本含量的大小確定“組段”數,一般設8-15個組段,觀察單位較少時組段數可相對少些,觀察單位較多時組段數可相對多些,常用全距的1/10取整做組距,以便於匯總和計算。第一組段應包括全部觀察值中的最小值,最末組段應包括全部觀察值中的最大值,並且同時寫出其下限與上限。各組段的起點和終點分別稱為下限和上限,某組段包含下限,但不包含上限,其
組中值為該組段的(下限+上限)/2。相鄰兩組段的下限之差稱為組距。
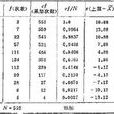
(3)列表劃記:確定組段界限,列成表2.1的形式,採用計算機或用
劃記法將原始數據匯總,得出各組段的觀察例數,即
頻數,表中的第(1)、(3)欄即所需的頻數表。
 頻數表
頻數表由頻數表可看出頻數分布的兩個重要特徵:
集中趨勢(central tendency)和
離散程度(dispersion)。身高有高有矮,但多數人身高集中在中間部分組段,以中等身高居多,此為集中趨勢;由中等身高到較矮或較高的頻數分布逐漸減少,反映了離散程度。對於
數值變數資料,可從集中趨勢和離散程度兩個側面去分析其規律性。
3.頻數分布的類型
頻數分布有對稱分布和
偏態分布之分。對稱分布是指多數
頻數集中在中央位置,兩端的頻數分布大致對稱。偏態分布是指頻數分布不對稱,集中位置偏向一側,若集中位置偏向數值小的一側,稱為
正偏態分布;集中位置偏向數值大的一側,稱為負偏態分布,如冠心病、大多數
惡性腫瘤等慢性病患者的年齡分布為負偏態分布。臨床上正偏態分布資料較多見。不同的分布類型應選用不同的統計分析方法。
4.頻數表的用途
可以揭示資料分布類型和分布特徵,以便選取適當的統計方法;便於進一步計算指標和統計處理;便於發現某些特大或特小的可疑值。
 頻數表
頻數表