設X是隨機變數,若E(Xk)(k=1,2,...) 存在,則稱它為X的k階原點矩,記作vk(X) 。
基本介紹
- 中文名:原點矩
- 外文名:origin moment
- 學科:數學
- 對象:隨機變數X
- 性質:一階為X的數學期望
- 相關名詞:中心矩
基本介紹
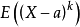
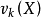
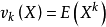
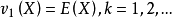
中心矩
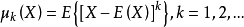
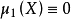
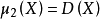
關係
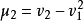
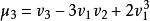
舉例
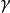
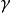
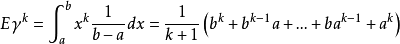
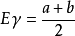
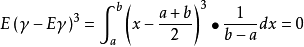
設X是隨機變數,若E(Xk)(k=1,2,...) 存在,則稱它為X的k階原點矩,記作vk(X) 。
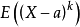
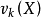
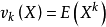
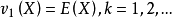
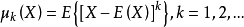
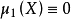
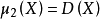
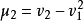
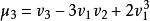
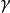
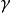
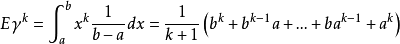
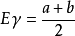
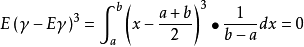
設X是隨機變數,若E(Xk)(k=1,2,...) 存在,則稱它為X的k階原點矩,記作vk(X) 。...... 原點矩顧名思義,是隨機變數到原點的距離(這裡假設原點為零點)...
中心矩:對於正整數k,如果E(X)存在,且E[|X-E(X)k]<∞,則稱E{[X-E(X)]k}為隨機變數X的k階中心矩。如X的方差是X的二階中心矩,即D(X)=E{[X-E...
矩是一個漢字,讀作ju/jǔ,本意是指曲尺,一種基本工具,可以畫直角形和方形,也可以測度直線長短或估量角度數,也指法度等。該文字在《離騷》和《孟子·離婁上》...
矩估計,即矩估計法,也稱“矩法估計”,就是利用樣本矩來估計總體中相應的參數。首先推導涉及感興趣的參數的總體矩(即所考慮的隨機變數的冪的期望值)的方程。然後...
在數學中,在試圖將一個度量μ映射到序列Mn時就產生了矩問題。矩問題(moment problem)指研究機率分布是否被其各階矩惟一決定的問題。在經典設定中,μ是實線上的...
有一類常用的統計量是樣本的數字特徵,他們是模擬總體數字特徵構造的,稱為樣本矩。樣本矩主要包括樣本均值、未修正樣本方差、樣本(修正)方差、樣本k階原點矩和樣本k...
k階矩是數學術語,隸屬於高等數學範疇。...... c=0時,稱其為X的k階原點矩;c=E[X]時,稱為k階中心矩。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次...
均方值(mean-square value)又稱X(t)的二階原點矩,是隨機變數X(t)的平方的均值,記為E[X2(t)] ,在工程上表示信號的平均功率,其平方根稱有效值。...
(4)樣本的K階原點矩: ;(5)樣本的K階中心矩: ;樣本值套用 編輯 用樣本來估計總體,通過對樣本特徵的研究來估計總體的特徵。這種機率統計的方法在市場調研、金融...
當以經驗分布函式代替F(x)時,總體的原點矩 的估計 ,恰好是祥本的同階原點矩。因此,用樣本原點矩代替總體矩是可行的,這是矩估計法的基本思想。...
均值函式即一階原點矩函式 過程的數學期望作為參數的函式。給定隨機過程 ,如果對於每個參數 t ,隨機變數 都是可積的,則稱 上的函式 為過程的均值函式。[1] ...
