格里汶科定理

格里汶科定理是指當樣本容量n→∞時，經驗分布函式以機率1一致收斂於總體的分布函式。格里汶科定理有重要理論意義，它溝通了經驗分布和理論分布，為統計推斷奠定了理論基礎。

基本介紹

• 中文名：格里汶科定理
• 外文名：Clivenko theorem
• 所屬學科：數學（統計學）
• 證明者：格里汶科(W. Clivenko)
• 相關概念：經驗分布函式，分布函式等

基本介紹

根據大數定律可知，事件發生的頻率依機率收斂到這個事件發生的機率，因此可用事件{X≤x}發生的頻率來估計P{X≤x}，即可用經驗分布函式來估計總體的理論分布F(x) =P{X≤x}，格里汶科(W. Clivenko)於1933年從理論上嚴格地證明了總體X的經驗分布函式和理論分布函式之間關係的結論，內容如下：

格里汶科定理 設總體X的分布函式為F(x)，經驗分布函式為F_n(x)，則有

即依機率1關於x均勻地收斂於，也即當n足夠大時，對於所有的x值，與之差的絕對值都足夠小的事件發生的機率等於1，這正是用樣本推斷總體的理論依據。圖1直觀地刻畫出了總體的分布函式（光滑曲線）與總體的經驗分布函式（階梯曲線）之間的關係，顯然當n足夠大時，可用很好地近似。

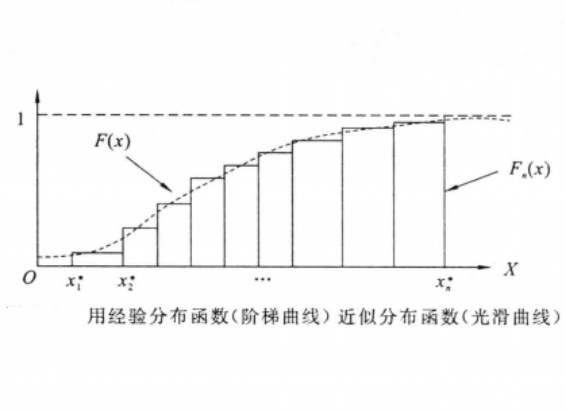
圖1 用經驗分布函式（階梯曲線）近似分布函式（光滑曲線）

格里汶科定理表明，當n充分大時，樣本分布函式近似地等於總體分布函式，又因隨機變數的各種數字特徵由其分布函式唯一確定，因此，當n充分大時，樣本的數字特徵，包括樣本均值，樣本方差及樣本各階矩，也就近似地等於總體的數字特徵。事實上，由大數定理可以證明，當n→∞時，樣本的數字特徵將收斂到總體的數字特徵(假定存在的話)，因此，格里汶科定理就是利用樣本來推斷總體分布及其數字特徵的理論依據。關於定理的證明請參考相應的參考資料。

格里汶科定理的套用

關於矩估計法的思想

格里泣科定理指出，當n→∞吋，經驗分布函式關於x均勻地依機率收斂於總體分布函式，這就使得在大祥本下可以用經驗分布函式代替F(x)研究統計推斷問題的理論依據。

當以經驗分布函式代替F(x)時，總體的原點矩的估計，恰好是祥本的同階原點矩。

因此，用樣本原點矩代替總體矩是可行的，這是矩估計法的基本思想。

在一般情況下，矩估計不是唯一的，如X服從泊松分布，是未知參數吋，可以用E(X)=，即祥本一階原點矩代替總體一階原點矩，也可以用D(X)=，即樣本二階中心矩代替總體二階中心矩。