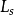系統簡介
在
排隊論的一般模型中,各個顧客由顧客源(總體)出發,到達機構(服務台、服務員)前排位等候接受服務,服務完了後就離開,佇列的數目和排列方式稱為排列結構,顧客按怎樣規則次序接受服務稱為排隊規則和服務規則。從服務到達接受服務以後離去,這一從到達到離去為止的過程就構成了一個排隊系統。
系統組成
排隊系統由輸入過程與到達規則、排隊規則、服務機構的結構、服務時間與服務規劃組成。
一般還假設到達間隔時間序列與服務時間均為獨立同分布隨機變數序列,且這兩個序列也相互獨立。
評價一個排隊系統的好壞要以顧客與服務機構兩方面的利益為標準。就顧客來說總希望等待時間或逗留時間越短越好,從而希望服務台個數儘可能多些但是,就服務機構來說,增加服務台數,就意味著增加投資,增加多了會造成浪費,增加少了要引起顧客的抱怨甚至失去顧客,增加多少比較好呢?顧客與服務機構為了照顧自己的利益對排隊系統中的3個指標:隊長、等待時間、服務台的忙期(簡稱忙期)都很關心。因此這3個指標也就成了排隊論的主要研究內容。
更具體的說,排隊系統包括顧客源、佇列、服務機構。可用下面圖來表達它們之間的關係:
現實世界中形形色色的排隊系統:
到達的顧客
| 要求服務的內容
| 服務機構
|
不能運轉的機器;
修理技工;
電話呼喚;
| 修理;
領取修配零件;
通話;
| 修理技工;
發放零件的管理員;
交換台;
|
排隊論的套用非常廣泛。它適用於一切服務系統。尤其在通信系統、交通系統、計算機、存貯系統、
生產管理系統等方面套用得最多。排隊論的產生與發展來自實際的需要,實際的需要也必將影響它今後的發展方向。
輸入過程
顧客源
(2)有限m(如車間裡待修理的機器)
到達規律
指到達間隔時間T 的分布:
分為: (1)定長 D (2)負指數 M(3)k階愛爾朗 Ek
排隊規則
損失制
指顧客到達時若所有服務實施均被占用,則顧客自動離去。
等待制
指顧客到達時若所有服務實施均被占用,則留下來等待,直至被服務完離去。
等待的服務規則又可分為:(1)先到先服務(FCFS)
(2)後到先服務(LCFS)
混合制
分為:(1)系統容量有限制
(2)等待時間有限制
服務機構
服務台個數 C:一般均為並列多台;
服務規律:指服務時間 v 的分布
分為:(1) 定長 D
(2)負指數 M
(4) 一般分布 G
模型表示
用記號(X/Y/Z/A/B/C)表示,其中
X:顧客到達時間間隔的分布
Y:服務時間的分布
Z:服務台個數
A:系統容量
B:顧客源數量
C:服務規則
衡量指標
服務隊長Ls—服務中的顧客數;
排隊長Lq—佇列中的顧客數;
總隊長L=Ls+Lq 系統中的顧客總數;
逗留時間Ws—顧客在服務中的等待時間;
等待時間Wq—顧客在佇列中的等待時間;
總時間W=Ws+Wq 顧客在系統中的總停留時間;
忙期—服務機構兩次空閒的時間間隔;
服務強度ρ;
穩態—系統運行充分長時間後,初始狀態的影響基本消失,系統狀態不再隨時間變化。
問題求解
主要是計算描述系統運行狀態的指標:
1. 隊長和排隊長
隊長:系統中的顧客數;其機率分布稱狀態機率,記為
,表示系統中有n個顧客的機率;隊長的平均值記為
。
2.逗留時間和等待時間
逗留時間:一個顧客在系統中的停留時間,記為W,其均值記為Ws。
等待時間:一個顧客在系統中排隊等待的時間,記其均值為Wq 。
到達的規律
描述顧客到達規律可從兩方面:
現實中有許多服務系統,其顧客的到達具有下述特徵:
(1)無後效性:任一時段的到達數不受前一時段的影響;
(2)平穩性:顧客到達是均勻的;
(3)稀有性:瞬時內只可能有1個顧客到達。
稱具有上述特徵的輸入為泊松流,其在 t 時段內到達n個顧客的機率服從
泊松分布。
服務的規律
主要討論服務時間 v 服從負指數分布的情形,參數為
,即
由於v 的均值為
,即平均對每位顧客的服務時間為
,可得參數的含義:服務率,即單位時間平均服務完人。