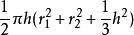弓形:由弦及其所對的弧組成的圖形叫做弓形。
弦AB把圓分成兩部分,這兩部分都是弓形.弓形是最簡單的組合圖形.
當弓形的弧小於半圓時,術語名稱為“劣弧弓”,其面積等於扇形面積與三角形面積的差;nπr^2/360-ad/2
當弓形的弧大於半圓時,術語名稱為”優弧弓“,其面積等於扇形面積與三角的面積的和:nπr^2/360+ad÷2
當弓形弧是半圓時,術語名稱為”半圓弓“,其面積是圓面積的一半。
基本介紹
- 中文名:弓形
- 外文名:arch
- 提出者:未知
- 提出時間:約1950年
- 套用學科:數理科學
幾何定義

幾何公式
弓形面積公式
相關概念