基本介紹
- 中文名:相似弓形
- 外文名:similar segments of a circle
- 所屬學科:數學(平面幾何)
- 簡介:含相等角的弓形
- 性質:相等的弦上的相似弓形全等
基本介紹,相關結論,相似弓形的面積,
基本介紹
相似弓形是那些含相等角的弓形,或者張在它們上的角是彼此相等的。
弓形是由一條弦和一段弧所圍成的圖形;弓形的角是由一直線和一段圓弧所夾的角;
在一段圓弧上取一點,連線這點和這段圓弧的底的兩個端點的二直線所夾的角叫做弓形角,而且把這個弓形角叫做張於這段弧上的弓形角;由頂點在圓心的角的兩邊和這兩邊所截--段圓弧圍成的圖形叫做扇形。
相關結論
命題1 在同一條線段的同一側,不可能作兩個相似但不相等的弓形。
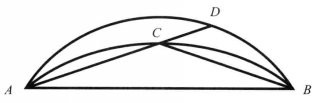 圖1
圖1假設可能,設在同一線段ABV的同一側作相似且不相等的弓形ACB、弓形ADB,作ACD與兩弓形相交,連線CB、DB。
那么因為:弓形ACB相似於弓形ADB,而圓的相似弓形有相同的角。
所以:∠ACB等於∠ADB,即是外角等於內角,這是不可能的。
所以:在同一條線段的同一側,不可能作兩個相似但不相等的弓形。
證完。
命題2相等的弦上的相似弓形全等。
設:AEB、CFD為作在相等線段AB、CD上的兩個相似弓形。
求證:弓形AEB全等於弓形CFD。
因為,如果弓形AEB移動到CFD,且A點放置在C點,線段AB線上段CD上,那么,點B就與點D重合。因為AB等於CD,AB又與CD重合,弓形AEB也就與弓形CFD重合。
因為:如果線段AB與CD相重合,而弓形AEB與弓形CFD不相重合,那么它或者落於其內,或者落於其外,或者落在CGD的位置,則兩圓相交形成兩個以上的交點。這是不可能的。
所以:如果線段AB重疊在CD上,那么弓形AEB就不能不與CFD重合。所以:它們全等。
所以:相等弦上的相似的弓形全等。
相似弓形的面積
求月牙形面積
希俄斯島的希波克拉底比阿那克薩哥拉稍微年輕一些, 最初大約來自希臘世界的同一地區。不要把他混同於另一位更有名的同時代人:科斯島的醫生希波克拉底。科斯和希俄斯都是多德卡尼斯群島中的島嶼;但希俄斯島的希波克拉底大約在公元前430年離開了故鄉,以一個商人的身份去了雅典。亞里士多德說,希波克拉底不如泰勒斯精明,他在拜占庭因為騙局而血本無歸;另有人說,他遭到了海盜的圍攻。不管怎樣吧,受害人從未對這件事情感到遺憾,因為他把這視為自己的好運,結果讓他轉向了幾何學研究,在這方面,他取得了引人注目的成就一這 是一個典型的英雄時代的故事。普羅克洛斯曾寫到,希波克拉底編寫過一部《幾何原理》,比歐幾里得那部赫赫有名的《幾何原本》早100多年。然而,希波克拉底的這部教科書一也有傳聞說是柏拉圖學派晚期的一位同人利昂所寫一失傳了, 儘管亞里士多德知道這本書。事實上,公元前5世紀的數學論文無一倖存;但我們有一個希波克拉底的著作片段,對此,辛普里丘(約520年在世)聲稱是從歐德謨斯的《數學史》(History of Mathematics,今已失傳)中逐字抄錄的。這段簡短的陳述,是我們所能得到的最接近於那一時期數學原始材料的東西,它描述了希波克拉底作品中處理求月牙形面積的部分。月牙形是由兩段半徑不等的圓弧所圍起來的幾何圖形,求月牙形面積的問題無疑源自於化圓為方問題。歐德謨斯的片段把下面這條定理歸到了希波克拉底名下:
相似弓形的面積之比等於其底邊的平方之比。
歐德謨斯的記述稱,希波克拉底首先指出,兩個圓的面積之比等於各自直徑的平方之比,從而證明了上述定理。這裡,希波克拉底採用了在畢達哥拉斯思想中扮演了極為重要角色的比例的語言和概念。事實上,有人認為,希波克拉底也成了一個畢達哥拉斯的信徒。克羅頓的畢達哥拉斯學派遭到了取締(可能是因為它的秘密性,也可能是因為它保守的政治傾向),但它的信徒卻散落各地,遍及整個希臘世界,這只不過起到了擴大該學派影響的作用。希波克拉底無疑(直接或間接地)感覺到了這種影響。
希波克拉底關於圓面積的定理,似乎是希臘世界中最早的對曲線求積法的準確陳述。歐德謨斯相信,希波克拉底給出了這一定理的證明,但嚴格的證明在那一時期( 即公元前430年前後)似乎是不大可能的。在這一階段,比例論大概僅僅是為可公度量而建立的。歐幾里得第二十二卷第2節中所給出的證明,源自於歐多克索斯,因此下面這個假設看來是合理的:《幾何原本》第三和第四卷中的很多公式源自於希波克拉底的作品。而且,如果希波克拉底給出了這個關於圓面積定理的證明,那么有可能就是他把間接的證明方法引入了數學。也就是說,兩個圓的面積之比等於(或不等於)其直徑平方之比。通過對兩種可能性的第二種作歸謬法,唯一可選的證明得以確立。
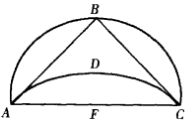 圖4
圖4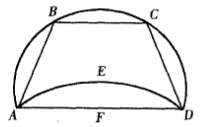 圖5
圖5從這個關於圓面積的定理,希波克拉底輕而易舉地發現了數學史上第一個求曲線區城面積的嚴謹方法。他從一個內接等腰直角三角形的半圓開始,在底(斜邊)上作出了一個與直角三角形邊上的圓弓形相似的弓形(圖4)。因為這些弓形的面積之比等於其底的平方之比,由直角三角形的畢達哥拉斯定理可知,兩個小弓形之和等於大弓形。因此,半圓AC與弓形ADCE之差等於三角形ABC。所以,月牙形ABCD正好等於三角形ABC;由於三角形ABC等於AC一半的平方,月牙形面積的求法也就找到了。
歐德謨斯還描述了一種基於等腰梯形的希波克拉底月牙形面積求法,內接於圓的等腰梯形ABCD,其最長邊(底) AD的平方等於三個較短邊AB、BC和CD的平方之和(圖5)。那么, 如果在邊AD上作一個弓形AEDF相似於三個等邊上的弓形,則月牙形ABCDE等於等腰梯形ABCDF。
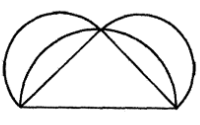 圖6
圖6下面這個事實表明,我們在描述希波克拉底的月牙形面積求法時,是有著相對可靠的歷史根據的:除了辛普里丘之外,還有別的學者也提到了這項工作。辛普里丘生活在6世紀,但他所依據的並不僅僅是歐德謨斯(約公元前320年在世),而且還有亞里士多德的主要注釋者之一、阿芙洛蒂斯的亞歷山大(約公元200年在世)。亞歷山大描述了兩種不同於,上述方法的月牙形面積求法。(1) 如果分別在等腰三角形的斜邊和直角邊上作半圓(圖6),那么,在較短邊上所創造出來兩個月牙形之和就等於三角形。(2)如果在一個半圓的直徑上作一個三邊相等的等腰梯形(圖7),並在三條等邊上作半圓,則梯形的面積就等於四個曲線區域的面積之和;三個月牙形和梯形等邊上的一個半圓。從第二種月牙形面積求法可以得出:如果能求出與月牙形面積相等的正方形,那么,與半圓——因此也包括圓——相等的正方形也是可以求出的。這個結論似乎鼓勵了希波克拉底,還有他的同時代人和早期繼任者,使之滿懷信心地希望最終能夠求出與圓面積相等的正方形。
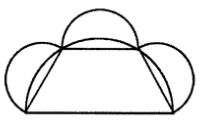 圖7
圖7