幾何弧是一條平面曲線,它是圓上兩點間的一段,包含兩個端點。
若圓心位於弧與弦連線成的封閉圖形之內,這段弧稱為優弧。若圓心位於弧與弦連線成的封閉圖形之外,這段弧稱為劣弧。
基本介紹
- 中文名:幾何弧
- 外文名:geometry arc
- 學科:數學
優弧、劣弧
幾何弧的長度



幾何弧半徑



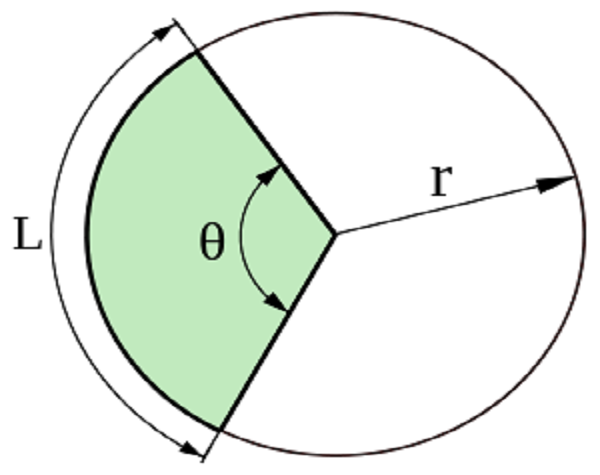
幾何弧是一條平面曲線,它是圓上兩點間的一段,包含兩個端點。
若圓心位於弧與弦連線成的封閉圖形之內,這段弧稱為優弧。若圓心位於弧與弦連線成的封閉圖形之外,這段弧稱為劣弧。






幾何弧是一條平面曲線,它是圓上兩點間的一段,包含兩個端點。若圓心位於弧與弦連線成的封閉圖形之內,這段弧稱為優弧。若圓心位於弧與弦連線成的封閉圖形之外,這段弧稱為劣弧。優弧、劣弧優弧是指圓心位於弧與弦連線成的封閉圖形之內;...
1.頂點在圓心上的角叫做圓心角(central angle),圓心角度數等於所對的弧的度數。2. 頂點在圓周上,且它的兩邊分別與圓有另一個交點的角叫做圓周角。圓周角等於相同弧所對的圓心角的一半,等於所對的弧的度數的一半。等圓 能夠重合的兩個圓叫做等圓。同心圓 圓心相同的圓叫做同心圓。同圓 半徑相同的圓叫做...
③在同圓或等圓中,相等的弧所對的圓周角等於它所對的圓心角的一半(圓周角與圓心角在弦的同側)。④如果一條弧的長是另一條弧的2倍,那么其所對的圓周角和圓心角是另一條弧的2倍。全等判定 全等多邊形 概念:全等多邊形的對應邊、對應角相等。判定:對應邊、對應角分別相等的兩個多邊形全等。全等三角形 (1...
幾何是研究空間結構及性質的一門學科。它是數學中最基本的研究內容之一,與分析、代數等等具有同樣重要的地位,並且關係極為密切。 名稱由來 幾何藝術幾何一詞最早起源於希臘語“γεωμετρία”,由“γέα”(土地)和“μετρεĭν”(測量)兩個詞合成而來,指土地的測量,即測地術。後來轉化為拉丁...
經典幾何圖形是經典幾何種常用的圖形元素,主要有矩形,三角形,圓等。矩形 定義 矩形(rectangle)是一種平面圖形,矩形的四個角都是直角,同時矩形的對角線相等,而且矩形所在平面內任一點到其兩對角線端點的距離的平方和相等。性質 1.矩形的四個角都是直角 2.矩形的對角線相等 3.矩形所在平面內任一點到其兩...
平面幾何圖形 可分為以下幾類:(1)圓形:包括正圓,橢圓,多焦點圓——卵圓。(2)多邊形:三角形、四邊形、五邊形等。(3)弓形:優弧弓、劣弧弓、拋物線弓等。(4)弧形:月牙形、穀粒形、太極形、葫蘆形等。套用 幾何圖形的套用非常廣泛,無論在設計、繪畫創作、數學研究中都需要藉助幾何圖形進行。數學定義...
一條母線繞著一條軸線作螺旋運動(等速旋轉和等速軸向移動)而形成的曲面,稱為螺旋面(Helicoidal Surface)。常見的螺旋面有正螺旋面、斜螺旋面(阿基米德螺旋面)、sincos螺旋面、漸開螺旋面等。與螺旋線一樣,螺旋面也有右旋與左旋之分。介紹 螺旋面是一類常見的曲面。以螺旋線和它的軸線為導線,直母線(也可以...
幾何基元 幾何基元(geometric primitive)是2012年公布的地理信息系統名詞,出自《地理信息系統名詞》第二版。定義 構成幾何圖形的基本元素。包括點、線、多邊形。出處 《地理信息系統名詞》第二版。
已知:∠AOB.求作:∠A'O'B',使∠A'O'B'=∠AOB.尺規作一個角的角平分線 已知:∠AOB.求作:射線OC,使∠AOC=∠BOC 作法:1.在OA和OB上分別截取OD,OE,使OD=OE.2.分別以D,E為圓心、以大於 DE的長為半徑作弧,兩弧在∠AOB內交於點C.3.作射線OC.OC就是∠AOB的平分線.
規定:(1)自變數x增大的方向為曲線的正向;(2)當弧段MₒM的方向與曲線正向一致時,M₀M的弧長S>0;相反時,S<0。術語介紹 弧微分的幾何意義是用一條線段的長度來近似代表一段弧的長度。MT的長度即為弧MM'的微分,由此聯繫勾股定理可得弧微分公式 故 特別地,當曲線由參數方程 給出時,有 當曲線由極...
幾何子的概念來源於Biederman(1987)在Marr和Nishihara(1978)的理論的基礎上提出的成分識別理論(recognition-by component theory)幾何子的概念來源於Biederman(1987)在Marr和Nishihara(1978)的理論的基礎上提出的成分識別理論(recognition-by component theory)。該模型基於這樣一種觀點,通過把複雜對象的結構拆分為稱做...
弧長公式是平面幾何的基本公式之一。弧長公式敘述了弧長,即在圓上過兩點的一段弧的長度,與半徑和圓心角的關係。公式為:l=πr|α|/180或l=πd|α|/360。在弧度制中,公式為:l=|α|r。基本公式 在半徑為 的圓上有一弧(圖一),設以 表示它的長,表示它所對的圓心角,表示直徑,則 這公式右端的 ...
圓在幾何圖形中可以說是一種非常常用的圖形,通過圓能夠衍生出很多曲線問題,圓弧就是最簡單的一種,用幾何畫板圓工具可以很輕易地作出圓,也可以利用幾何畫板構造圓上的弧,即構造圓弧。找圓心 任意一條圓弧可以找出它所在的圓里的圓心,方法如下:(1)首先,在圓弧上任意取3點A、B、C;(2)連線AB/BC形成兩...
弧形構造(arc structure)是一廣泛出現的構造類型,包括聯合弧、限制弧、牽引弧,以及邊緣弧、疊弧(套弧)、山字型構造的前弧與反射弧等。它們有不同成因,屬於不同構造體系或自成體系。中國境內比較典型的弧形山系有青藏高原東北緣、南大巴山、南天山、雪峰山和西崑侖-帕米爾弧型造山帶等。弧形構造幾何學特徵 ...
∴弧AC=弧BC 推導定理 推論一:平分弦(非直徑)的直徑垂直於這條弦,並且平分這條弦所對的兩段弧。幾何語言:∵DC是直徑,AE=EB ∴直徑DC垂直於弦AB,劣弧AD=劣弧BD,弧AC=弧BC 推論二:平分弦所對的一條弧的直徑垂直平分這條弦,並且平分這條弦所對的另一條弧。幾何語言:∵弧AD=弧BD ∴CD垂直平分AB...
曲線,是微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。微分幾何就是利用微積分來研究幾何的學科。為了能夠套用微積分的知識,我們不能考慮一切曲線,甚至不能考慮連續曲線,因為連續不一定可微。這就要我們考慮可微曲線。但是可微曲線也是不太好的,因為可能存在某些曲線,在某點切線的方向不是...
反向大圓弧 反向大圓弧(great circular arcs of oppositelydirected)亦稱相反定向大圓弧.球面幾何的基本概念之一指在同一球面大圓上的定向相反的兩條有向大圓弧.
圓上任意兩點間的部分叫做弧。直徑的兩個端點分圓成兩條弧,每一條弧都叫半圓。大於半圓的弧叫優弧。小於半圓的弧叫做劣弧。弧的定義 圓上任意兩點間的部分叫做弧。用符號” ”表示弧。例如,圖1中以 為端點的弧.記作 ,讀作弧 。設半徑為 的圓中, °的圓心角所對的弧長為 ,則弧長公式為: ...
弧度,舊稱弳。在數學和物理中,弧度是角的度量單位。它是由國際單位制導出的單位,單位縮寫是rad。其定義為:弧長等於圓半徑的弧所對應的圓心角為1rad。根據定義,一周的弧度數為2πr/r=2π,360°=2π rad,因此,1rad約為57.3°。定義 用弧長和半徑之比度量圓心角的單位。弧長等於半徑的弧,其所對的...
圓上任意兩點間的部分叫做圓弧,簡稱弧。初、高中數學課有教學。圓的任意一條弦的兩個端點把圓分成兩條弧,所對圓心角小於180°的圓弧叫做劣弧,劣弧所對的圓心角是劣角;如概述圖,圓O中,通過觀察可知弧AB所對較小圓心角的那部分為劣弧。弧的定義 圓上任意兩點間的部分叫做圓弧,簡稱弧。弧是一條平面曲線,...
當弓形的弧小於半圓時,術語名稱為“劣弧弓”,其面積等於扇形面積與三角形面積的差;nπr^2/360-ad/2 當弓形的弧大於半圓時,術語名稱為”優弧弓“,其面積等於扇形面積與三角的面積的和:nπr^2/360+ad÷2 當弓形弧是半圓時,術語名稱為”半圓弓“,其面積是圓面積的一半。幾何定義 弦AB把圓分成兩部分...
定理內容:弧上的所有點中,弧的中點到弧兩端距離和最長。定律定義 弧上的所有點中,弧的中點到弧兩端距離和最長。幾何語言:如圖1,在☉ 中,弧 弧 , 。推導過程 【證法一】如圖2,延長 至點Q,使PQ=BP,連結BQ。則 ,且∠BQP= ∠P= ∠M,∴點Q在以M為圓心,MA為半徑的圓上,∴AQ的最大值...
同向大圓弧 同向大圓弧(same directed great circular arcs)亦稱相同定向大圓弧.球面幾何的基本概念之一指在同一球面大圓上的定向相同的有向大圓弧.
因此,在實際工程設計問題中,常用曲率圓在點M鄰近的一段圓弧來近似代替曲線弧,以使問題簡化。意義 曲率是幾何體不平坦程度的一種衡量。平坦對不同的幾何體有不同的意義。本文考慮基本的情況,歐幾里得空間中的曲線和曲面的曲率。一般意義下的曲率,請參照曲率張量。在動力學中,一般的,一個物體相對於另一個物體...
從字面上看,《弧線》是最簡單不過了,連國小二年級的學生也不會有文字關;從描繪的對象看,也只不過是生活中常見的四種現象——用形象的語言來表述,就是四種近似幾何中弧線的生活現象。正因為如此淺顯而且簡單,所以,這種文字是否成為詩也就是爭論的一個焦點。其次,如果是詩,那么它表明或暗示什麼呢?這也是...
頂點在圓上,一邊和圓相交,另一邊和圓相切的角叫做弦切角。其大小等於它所夾的弧所對的圓周角。定義 頂點在圓上,一邊和圓相交,另一邊和圓相切的角叫做弦切角。特徵識別 ①頂點在圓上;②一條邊與圓周相交,另一條邊與圓相切,切點在圓周上;③弦切角的大小等於它所夾的弧所對的圓心角的大小的一半。弦切角...
