圓上任意兩點間的部分叫做弧。直徑的兩個端點分圓成兩條弧,每一條弧都叫半圓。大於半圓的弧叫優弧。小於半圓的弧叫做劣弧。
基本介紹
- 中文名:優弧
- 外文名:major arc
- 所屬學科:數學
- 定義:大於半圓的弧叫優弧
- 相關概念:弧、劣弧等
弧的定義
 圖1
圖1優弧的定義


劣弧
半圓
弧的相關性質
相關命題舉例
 圖2
圖2 圖3
圖3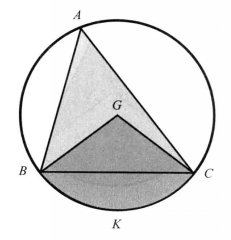 圖4
圖4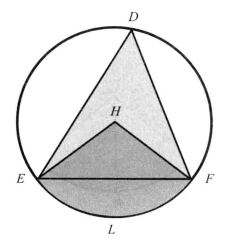 圖5
圖5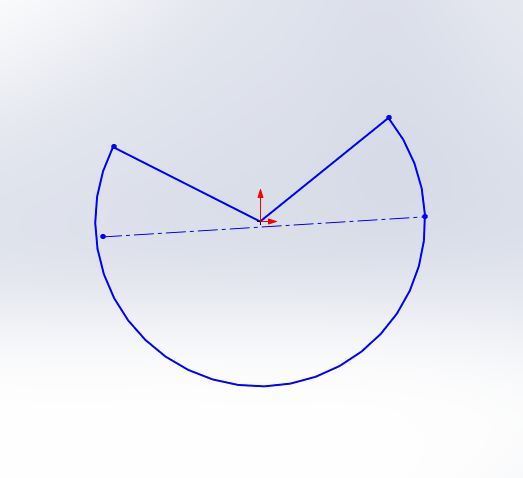
圓上任意兩點間的部分叫做弧。直徑的兩個端點分圓成兩條弧,每一條弧都叫半圓。大於半圓的弧叫優弧。小於半圓的弧叫做劣弧。
 圖1
圖1

 圖2
圖2 圖3
圖3 圖4
圖4 圖5
圖5圓上任意兩點間的部分叫做弧。直徑的兩個端點分圓成兩條弧,每一條弧都叫半圓。大於半圓的弧叫優弧。小於半圓的弧叫做劣弧。...
四川優弧聯創網路科技有限公司於2017年11月28日成立。法定代表人霍衝鋒,公司經營範圍包括:網路技術開發、技術諮詢、技術服務;基礎軟體服務;計算機軟體開發;機械設備研發...
北京優弧文化傳媒有限公司於2001年01月08日成立。法定代表人唐浩,公司經營範圍包括:企業文化藝術交流活動;代理、發布廣告;承辦展覽展示活動;經濟信息諮詢等。...
幾何弧是一條平面曲線,它是圓上兩點間的一段,包含兩個端點。若圓心位於弧與弦連線成的封閉圖形之內,這段弧稱為優弧。若圓心位於弧與弦連線成的封閉圖形之外,...
1 定義 ▪ 弧與弧長 ▪ 優弧與劣弧 2 公式 弧定義 編輯 弧弧與弧長 弧的定義:圓上任意兩點之間的部分。弧的大小的兩種表示:弧長與弧度。弧長...
小於半圓的弧叫劣弧,大於半圓的弧叫優弧。弧〈名〉(形聲。從弓,從瓜,瓜亦聲。“瓜”指“滾瓜”。“弓”與“瓜”聯合起來表示“弓張滿後可以在上面滾瓜”...
大於半圓的弧稱為優弧,小於半圓的弧稱為劣弧。圓周上任意兩點分圓周成兩條弧。若不特別聲明,一般常指一段劣弧。圖1 象限弧套用--象限儀 編輯 ...
優弧是指圓心位於弧與弦連線成的封閉圖形之內;劣弧是指圓心位於弧與弦連線成的封閉圖形之外。簡單地說,大於半圓的弧即是優弧,而小於半圓的弧就叫劣弧。半圓則沒...
弧線,數學用語。圓上任意兩點間的部分叫做圓弧,簡稱弧(arc)。大於半圓的弧稱為優弧,小於半圓的弧稱為劣弧。半圓既不是優弧,也不是劣弧。...
圓弧是一個漢語辭彙,拼音是yuán hú,圓上任意兩點間的部分叫做圓弧,簡稱弧。初、高中數學課有教學。圓的任意一條直徑的兩個端點把圓分成兩條弧,大於半圓叫優弧...
倡導局部設計與整體美容相協調的統一理念,尤其擅長美胸塑形和面部整形,在優弧彈態美胸、多維美雕鼻部綜合整形和眼部精微綜合整形的手術上有著極高的造詣。...
∴DC是圓的直徑,劣弧AD等於劣弧BD,優弧ACO=優弧BCO推論三:平分弦所對的一條弧的直徑垂直平分這條弦,並且平分這條弦所對的另一條弧。...
當弓形的弧大於半圓時,術語名稱為”優弧弓“,其面積等於扇形面積與三角的面積的和:nπr^2/360+ad÷2 當弓形弧是半圓時,術語名稱為”半圓弓“,其面積是圓面積...
把弓形弧兩端與圓心連結得一個扇形和一個三角形,當弓形弧為劣弧時,弓形面積等於扇形面積減去三角形面積;當弓形弧為優弧時,弓形面積等於扇形面積加上三角形面積 [1...
▪ 163°C的淡黃優弧 ▪ 360°C的淡黃原點 4 人物簡介 5 詩詞選 劉童作品年表 編輯 曾在馬來西亞以及國內國內各大雜誌開設專欄,07-08年度在《完全生...
圓內接正五邊形的五條邊在圓內所對的五條優弧長度相等 圓內接正五邊形的五條邊在圓內所對的五條優弧的弧度數相等 圓的五等分及圓內接五邊形作法作圖...
