定義運算
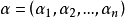
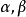
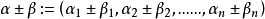


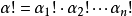
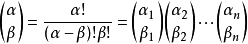
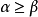
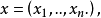

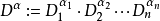
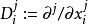
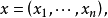

套用範圍
多元微積分
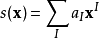

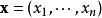
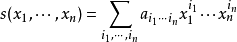
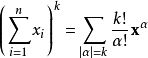

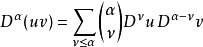
泰勒展開式: 對一多元解析函式 f,當

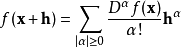
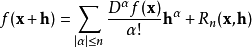
偏微分運算元
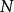

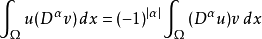
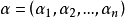
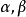
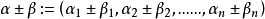


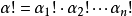
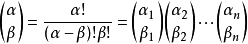
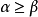
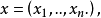

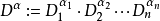
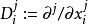
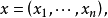

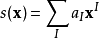

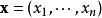
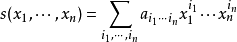
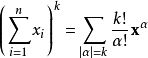

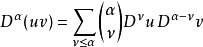

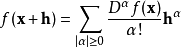
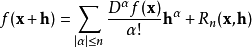
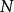

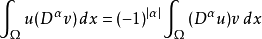
多重指標是數學中一種方便的表示法,它將指標中的單個整數推廣為多個整數,它可以簡化多元微積分、偏微分方程與分布理論中的計算,也便於操作冪級數。...
多重相關係數,亦稱復相關係數,指一個隨機變數與某一組隨機變數間線性相依性的度量。...
多重共線性是指線性回歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。一般來說,由於經濟數據的限制使得模型設計不當,導致...
多重線性回歸(multiple linear regression) 是簡單直線回歸的推廣,研究一個因變數與多個自變數之間的數量依存關係。多重線性回歸用回歸方程描述一個因變數與多個...
多重能力傾向測驗是由測各種不同能力的分測驗組成,可以一般地了解人的潛能方向。多重能力傾向測驗可以說是多種能力傾向測驗的複合體,包含著幾個不同性質的分測驗...
多重比較法是多個等方差正態總體均值的比較方法。經過方差分析法可以說明各總體均值間的差異是否顯著,即只能說明均值不全相等,但不能具體說明哪幾個均值之間有顯著...
多重平衡規則(Multiple equilibrium rules)是指如果某一可逆反應可以由幾個可逆反應相加(或相減)得到,則該可逆反應的標準平衡常數等於幾個可逆反應的標準平衡常數的...
模組是指電腦程式中具有相對獨立性的一組邏輯上有關的實體,能獨立完成某一個特定功能。多重模組訪問是指程式需要完成某種功能時需要嵌套調用其他模組的程式的功能...
所謂多重計量假設首先體現在環境會計中應該同時採用貨幣和非貨幣兩類計量形式。...... 貨幣計量為主,輔之以實物,與自然環境相關的實物指標、勞動指標、技術指標.甚至...
《數據的統計處理和解釋測試結果的多重比較(GB/T 10092-2009)》的附錄A為規範性附錄,附錄B為資料性附錄。本標準由全國統計方法套用標準化技術委員會(SAC/TC 21...
《中國森林多重效益項目設計標準與指標》是2007年中國林業出版社出版的圖書。...... 《中國森林多重效益項目設計標準與指標》是2007年中國林業出版社出版的圖書。...
MA指標分類 編輯 以時間的長短劃分,移動平均線可分為短期、中期、長期幾種,綜合觀察長、中、短期移動平均線,可以研判市場的多重傾向。如果三種移動平均線並列上漲,...
威廉指標撞頂的分析原則是指威廉曲線從低位上升到指標的超買區(20——0)後,經過一段時間的運行,曲線連續幾次撞及指標的頂部(0線)時,會局部形成多重頂的形態,...
WR連續幾次撞頂(底),局部形成雙重或多重頂(底),是買進(賣出)的信號。 [1] wR指標注意事項 1頂背離當股價K線圖上的股票走勢一峰比一峰高,股價在一直向上...
W&R指標是一種利用振盪點來反映市場超買超賣現象,預測循環周期內的高點和低點,...W&R連續幾次撞頂(底),局部形成雙重或多重底(頂)則是(進貨)出貨的信號。...
W&R連續幾次撞頂(底),局部形成雙重或多重頂(底),是賣出(買進)的信號。同時,使用過程中應該注意與其他技術指標相互配合。在盤整的過程中,W&R的準確性較高,...
第五個方面,KD指標曲線的形態。當KD指標在較高或較低的位置形成了頭肩形和多重頂(底)時,是採取行動的信號。這裡股票投資者同樣需要注意的是,這些形態一定要在...
交錯多重線性映射(alternating multilinear mapping)是一種特殊的反對稱多重線性映射。其定義是:設映射f∈£p(E;F),如果只要至少對於一個指標i(1≤i
二、指標體系建構的多重矛盾三、指標體系建構的制衡問題四、指標體系建構的審慎認知第二十一章 指標反映的現實問題一、生活質量各領域的重要性與滿意度...
記者:有時候,人們發現,同樣一種食品,同樣一種成分,這個部門有一套標準,那個部門也有一套標準,專家們的說法也不盡相同。關於食品安全,我們國家是否存在多重標準?...
【操作性】:整體操作規範化,各類指標的計算方法和結果口徑統一。 【科學性】:指數模型公開、有效權重公正、評價結果公平。 【真實性】:標準的數據計算,多重數據質量...
