單連通空間

在拓撲結構中，拓撲空間被稱為簡單連線（或單連通），如果它是路徑連線的，並且兩點之間的每條路徑都可以連續變換，停留在空間內其他這樣的路徑，同時保留有問題的兩個端點。

如果一個空間不是簡單的連線，那么測量它不能簡單連線的程度是很方便的。這是由基層組織完成的。直觀地，基本組測量孔如何在空間上行為；如果沒有漏洞，基本組是平凡的 - 等價地，空間是簡單的連線，即為單連通空間。

基本介紹

• 中文名：單連通空間
• 外文名：simply connected space
• 領域：拓撲學
• 學科：數理科學
• 單連通：拓撲空間的一種性質
• 拓撲空間：簡單連線或單連通

定義

單連通空間(simply connected space)一類重要的拓撲空間.基本群為平凡群的道路連通空間稱為單連通空間.從而可推出可縮空間是單連通空間，但是其逆不一定成立.例如，歐氏空間中的凸集和n維球面S" (n,2)都是單連通空間，但n維球面S"(n,2)不是可縮空間.道路連通空間是單連通的充分必要條件是，此空間中任意兩條起點和終點分別相同的道路是同倫的.

非正式討論

非正式地說，如果我們的空間中有一個厚實的物體是由一塊構成的，並且沒有任何“洞”貫穿它，那么它就是簡單的連線。例如，既不是甜甜圈也不咖啡杯（帶把手）被簡單地連線，但中空的橡膠球被簡單地連線。在二維中，一個圓不是簡單的連線，而是一個圓盤和一條線。被空間連線，但不是簡單的連線被稱為非簡單的連線，或者在一個有點老式的長期，多重連線。

圖1 示意圖

圖1中，一個球體被簡單地連線起來，因為每一個環都可以被收縮（在表面上）到一個點上。

為了說明簡單連通的概念，假設我們正在考慮一個三維的對象;例如，盒子形狀的物體，麵包圈或開瓶器。把這個物體想像成一個形狀奇特的水族箱，裡面裝滿了水，兩邊都是剛性的。現在想想一個潛水員拿一根長繩子，以任何方式在水族箱裡面的水裡落下來，然後把繩子的兩端連線起來，形成一個閉環。現在循環開始收縮，變得越來越小。（假設這個循環魔術般地知道最佳的收縮方式，如果它可能避開它們的話，不會在鋸齒狀的邊緣上掛鈎）。如果循環可以一直收縮到一個點，那么水族館的內部是簡單地連線。如果有時環路被卡住了，例如在甜甜圈的中心孔周圍，那么物體就不是簡單的連線。

注意這個定義只排除了“手柄形”的孔。一個球體（或者相當於一個中空的橡皮球）是簡單的連線的，因為球體表面上的任何環都可以收縮到一個點上，儘管它在中空的中心有一個“孔”。更強的條件，物體沒有任何尺寸的洞，被稱為收縮性。

公式

這一套不是簡單的連線，因為它有洞。

甲拓撲空間X被稱為簡單地連線，如果它是路徑連線，並且任何連續地圖˚F：S→X（其中S表示單位圓中歐幾里德2空間）可以收縮以在以下意義上的點：存在連續映射F：D→X（其中D表示歐幾里德2-空間中的單位盤），使得限於SF為f。

一個等價的表達式是這樣的：若且唯若它是路徑連通的時候，X是簡單連通的，並且每當p：[0,1]→X和q：[0,1]→X是兩條路徑（即：連續映射）（p（0）=q（0）和p（1）=q（1）），那么p和q是同位相對{0,1}。直觀地說，這意味著p可以“連續變形”來獲得q，同時保持終點固定。因此，這個詞簡單地連線在一起：對於任何兩個給定的點X，有一個“本質上”只有一條路徑連線它們。

表達相同的第三種方式：若且唯若X是路徑連線的，並且每個點上的X的基本組是平凡的，即僅由標識元素組成時，X是簡單連通的。類似地，若且唯若X是所有態射集合中的所有點x，y時，X才被連線在基本的廣群的X只有一個元素。

在複雜分析中經常使用另一個公式：若且唯若黎曼球中的X和它的補數都連通時，C的開子集X是簡單連通的。

虛數部分嚴格大於零且小於1的複數的集合提供了一個無限的，連通的，開放的補集未連線的平面子集的一個很好的例子。它是簡單地連線。也許值得指出的是，放寬X連線的要求會導致對連線擴展補數的平面的開放子集進行有趣的探索。例如，一個（不一定是連線的）開放式集合在每個連線的組件都被簡單地連線時就準確地連線了擴展式互補。

示例

圓環不是簡單的連線。沒有任何一個彩色的圈可以收縮到一個點，不離開表面。

• 的歐幾里得平面- [R被簡單地連線，但ř減去原點（0,0）則不是。如果n> 2，則R和R兩者都減去原點。
  
• 類似地：若且唯若n≥2時，n維球面S是簡單地連通的。
  
• R每個凸子集都被簡單地連線起來。
  
• 甲環面，所述（橢圓）氣缸，所述莫比烏斯帶，所述投影面與克萊因瓶不是簡單地連線。
  
• 每個拓撲向量空間是簡單連線的;這包括Banach空間和Hilbert空間。
  
• 對於Ñ≥2時，特殊正交群SO（Ñ，- [R）不是簡單地連線和特殊酉群SU（Ñ）是簡單連線。
  
• 的長行大號是簡單連線，但它的緊湊化，延伸的長行大號*不是（因為它是不連通路連線）。
  
• 同樣，R的單點緊化不是簡單連線（即使R簡單連線）。
  

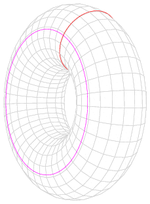圖3 圓環連線

屬性

一個曲面（二維拓撲流形）是連通的，若且唯若它連通且它的屬為0時。直觀上，該屬是曲面的“手柄”數。

如果一個空間X是不簡單連線，經常可以通過使用其糾正這一缺陷普遍罩，映射到一個簡單連線的空間X在一個特別好的方式。

如果X和Y是同倫等價的而X是簡單的連線，那么Y也是。

請注意，連續函式下的簡單連線集的圖像不需要簡單連線。以指數映射下的複平面為例：圖像是C- {0}，顯然不是簡單的連線。

簡單連通性的概念在複雜的分析中很重要，因為以下事實：

• 如果ü是的簡單連線的開子集複平面Ç，和˚F：ü→Ç是一個全純函式，然後˚F具有原函式˚F上ü，和每一個的值線積分在ü與積˚F僅取決於路徑的終點u和v，並且可以被計算為F（v）-F（u）。積分因此不依賴於連線u和v的特定路徑。
  
• 的黎曼映射定理指出的任何非空開單純連線子集Ç（除了Ç本身）是共形等效到單元盤。
  

簡單連通性的概念也是龐加萊猜想中的一個關鍵條件。