賽費特纖維空間(Seifert fibre spaces)亦稱賽費特流形。一類特殊的3維流形。除了3維球面與透鏡空間以外,賽費特纖維空間是一類較為具體,研究得較多的3維流形,而且它在3維流形上的齊性幾何(即常曲率幾何)中扮演著重要的角色。
基本介紹
- 中文名:賽費特纖維空間
- 外文名:Seifert fibre spaces
- 領域:數學
- 學科:幾何
- 別稱:賽費特流形
- 性質:一類特殊的3維流形
簡介,詳細釋義,3維流形的幾何,透鏡空間,
簡介
賽費特纖維空間(Seifert fibre spaces)亦稱賽費特流形。一類特殊的3維流形。除了3維球面與透鏡空間以外,賽費特纖維空間是一類較為具體,研究得較多的3維流形,而且它在3維流形上的齊性幾何(即常曲率幾何)中扮演著重要的角色。一個3維流形M,若它能表示為M中一些互不相交的簡單閉曲線之並,則稱為賽費特纖維空間,這些閉曲線稱為M的纖維。
詳細釋義
若對於其中的一個纖維c,取c在M中的正則鄰域N(c),可以要求N(c)由M中的一些纖維所構成,則把N(c)看做獨立於M之外的流形,有N(c)=B×S,而當N(c)按原來的方式放回到M時,對於N(c)上的一個纖維c′,在B×S上可以表示為λμ,其中λ代表π1(B×S)中的生成元S,μ代表其中的生成元B.當n=±1時,稱c為正則的,否則c稱為奇異的。由於在奇異纖維附近的纖維都是正則的,當M為緊緻流形時,M中僅有有限個奇異纖維,M為正則纖維之並。現在對M的研究,可著眼於這些奇異纖維上,通過適當調整c′的取向,總可假定n>0,0≤m≤n/2。若將M中每條纖維等同為一個點,則得軌道空間S,以及射影η:M→S。由於η(N(c))為S中的一個2維胞腔,從而表明S為2維流形,稱為M的伴隨賽費特曲面。設M有奇異纖維cα1,cα2,…,cαq,B1,B2,…,Bq為η(cα1),η(cα2),…,η(cαq)在S中互不相交的2維胞腔鄰域。若S=S-∪Int Bi, M=η(S),則η|M:M→S為通常意義下的纖維叢映射。若S≠0(當M無奇異纖維時,把一個正則纖維看做奇異即可),則S可收縮為圓周的一點並,因此η|M:M→S有截面,選η(Bi)的生成元ci,ti,其中ti為M上正則纖維,ci與ti相交於一點。另一方面,已有η(Bi)的生成元μi,λi,而ti=μiλi(當cαi為(mi,ni)型奇異纖維時),所以ci=μiλi,其中simi-rini=1, μi=tici,這樣可以由π1(M)中增加關係tici=1而計算π1(M)。具體說來,由范卡彭定理易知有下列結果:若M為有g個奇異纖維的賽費特纖維空間,其賽費特曲面S有虧格g以及k個邊界分支。
若賽費特纖維空間M為閉流形,則其中的賽費特結構可能不惟一,但是它上面的齊性幾何由兩個不變數決定,其一為賽費特曲面S的歐拉示性數χ,其二為M的歐拉示性數e。
3維流形的幾何
研究3維流形上的常曲率幾何。至今可以用三種方式來談論幾何,第一種:古典的歐氏幾何,在其中考慮點、線、面、角、長度等以及它們之間的相互關係,而且這種方法對於非歐幾何也適用;第二種:微分幾何;第三種是克萊因意義下的幾何,即考慮空間X與其上的—個可遷變換群G,所謂幾何(X,G)即考慮X在G之下的那些不變性.當然這三者只是立論不同而已,其內容有時是共通的。在這裡所論的幾何正是克萊因意義之下的幾何。由於流形M與它的泛覆疊空間X之間有相同的度量,所以為了討論流形M上的局部齊性度量,只須討論X上的齊性完備度量即可,其中G=Isom(X),即X上的保距群,並假定G有子群H,使得軌道空間(流形)X/H是緊緻的(稱為(X,G)有緊商).在這些限制之下,瑟斯頓(Thurston,W.P.)有下列定理:
1.任何單連通3維流形X上有緊商的完備齊性幾何(X,Isom(X))等價於下列8種幾何之一:
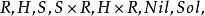
2.任何閉3維流形上,若有模型於上述意義下的幾何,則這種幾何是惟一的。
當然,瑟斯頓也注意到在閉3維流形的非平凡連通和之中,除了RP#RP以外,均無上述意義下的幾何,因此他的工作中也包含一些幾何猜想,即他認為任何緊緻、可定向3維流形,當用其中一些互不相交的球面與環面去切,並在球面的切口處再補上3維球體以後,必然有幾何結構。這些猜測之中包含著著名的龐加萊猜想,但是看來要證實它們還須走漫長的道路.在3維流形上存在常曲率幾何,這是近年來由瑟斯頓發展起來的一個新的研究課題,它對於流形性質的研究具有重要的意義。
透鏡空間
透鏡空間是一類特殊的可定向閉3維流形。有了3維閉流形的海嘎特分解與海嘎特圖概念以後,一個有趣的問題是,能否對於有某一固定虧格的海嘎特圖的流形進行分類。當虧格為1時,即對於分解(V,V′),其中V=V′為環面或克萊因瓶,賴德邁斯特(Reidemeister,K.W.F.)於1935年成功地進行了分類,所得到的閉3維流形是透鏡空間或S上的不可定向S叢。但是,對於虧格大於1的情形,至今尚無相應的結果。若V=S×B為環體,π1(V)是環面V的基本群,以S=a以及B=b為生成元,則V上的閉曲線ab為簡單閉曲線若且唯若p,q互素.於是,給定整數p,q,使得p≥0,(p,q)=1,則存在惟一3維閉流形Lp,q,它由海嘎特圖(V;J)決定,並且J為V上的簡單閉曲線,它在π1(V)中表示的元素為ab,這種流形稱為p,q型的透鏡空間。
