單峰函式是在所考慮的區間中只有一個嚴格局部極大值(峰值)的實值函式。如果函式f(x)在區間[a, b]上只有唯一的最大值點C,而在最大值點C的左側,函式單調增加;在點C的右側,函式單調減少,則稱這個函式為區間[a, b]上的單峰函式。
基本介紹
- 中文名:單峰函式
- 外文名:unimodal function
- 所屬學科:數學
- 相關概念:峰值點、谷值點、單谷函式等
概念
定義


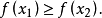
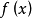
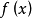
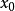
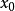
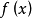
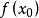
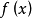
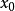

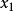
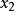

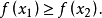
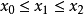
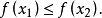
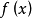
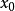
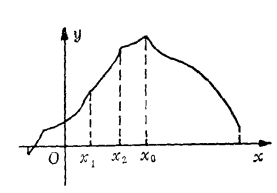 圖1
圖1 圖2
圖2實例分析



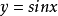
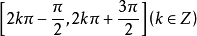
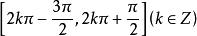

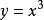
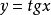
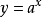
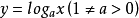
單峰函式的性質


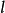
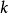
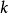
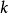
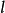
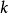










單峰函式的套用

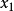
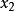
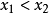
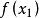
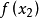

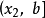
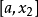


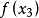
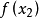

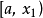
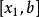
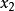
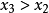
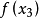
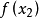





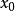

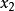

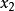
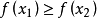
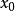
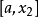

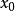
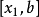

單峰函式是在所考慮的區間中只有一個嚴格局部極大值(峰值)的實值函式。如果函式f(x)在區間[a, b]上只有唯一的最大值點C,而在最大值點C的左側,函式單調增加;在點C的右側,函式單調減少,則稱這個函式為區間[a, b]上的單峰函式。


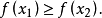
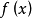
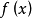
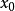
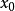
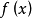
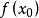
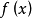
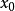

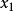
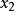

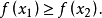
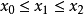
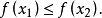
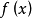
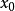
 圖1
圖1 圖2
圖2


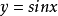
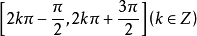
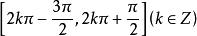

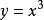
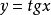
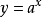
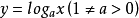


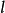
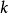











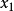
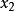
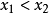
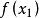
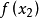

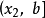
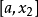


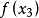
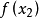

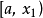
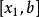
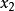
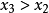
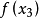
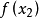





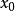

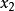

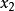
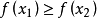
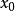
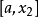

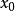
單峰函式是在所考慮的區間中只有一個嚴格局部極大值(峰值)的實值函式。如果函式f(x)在區間[a, b]上只有唯一的最大值點C,而在最大值點C的左側,函式單調...
單峰分配(Unimodal distribution)如果函式f(x)在區間[a, b]上只有唯一的最大值點(或最小值點)C,而在最大值點(或最小值點)C的左側,函式單調增加(減少);在...
斐波那契法(Fibonacci method),又稱Fibonacci法、斐波那契分數法,是一種一維搜尋的區間消去法。這種方法與0.618法(黃金分割法)類似,也是用於單峰函式,在計算過程中,...
成功失敗法(success-failure method)亦稱進退法、倍增半減法,是一種搜尋方法,為搜尋某區間上函式的極小(大)點,每次搜尋都要改變搜尋步長的一種方法,如果在第k次...
斐波那契搜尋(Fibonacci search) ,又稱斐波那契查找,是區間中單峰函式的搜尋技術。斐波那契搜尋就是在二分查找的基礎上根據斐波那契數列進行分割的。在斐波那契數列找一...
還是以區間(a,b)中的單峰函式f(x)為例。將(a,b)區間分成 等分,問題變為在(0, )範圍內求極值。第一次選擇 和 ,若保留下的區間是(0, ),則下次只需要...
伽瑪分布(Gamma Distribution)是統計學的一種連續機率函式,是機率統計中一種非常重要的分布。“指數分布”和“χ2分布”都是伽馬分布的特例。Gamma分布中的參數α稱...
線性規則 linear programming 具有非線性約束條件或目標函式的數學規劃,是運籌學的一個重要分支。...
濾波函式一般都是單峰函式。這個濾波函式就相當於遙感器的光譜回響函式。通俗的講:遙感器的光譜回響函式是波長的函式,是遙感器在每個波長處接收的輻亮度與入射的輻...
非線性規劃是一種求解目標函式或約束條件中有一個或幾個非線性函式的最最佳化問題的方法。運籌學的一個重要分支。20世紀50年代初,庫哈(H.W.Kuhn) 和托克 (A.W...
黃金分割搜尋是一種通過不斷縮小單峰函式 的最值的已知範圍,從而找到最值的方法。它的名稱源於這個算法保持了間距具有黃金分割特性的三個點。這個算法與斐波那契搜尋...
1.4 凸集與凸函式習題第二章 無約束最最佳化方法的一般結構2,1最優性條件2.2 線性搜尋2.2.1 精確線性搜尋2.2.2 搜尋區間與單峰函式...
7.1 簡單一元函式最佳化實例 1047.2 多元單峰函式的最佳化實例 1087.3 多元多峰函式的最佳化實例 1127.4 收穫系統最優控制 1157.5 裝載系統的最優問題 119...
