成功失敗法(success-failure method)亦稱進退法、倍增半減法，是一種搜尋方法，為搜尋某區間上函式的極小(大)點，每次搜尋都要改變搜尋步長的一種方法，如果在第k次疊代沿某方向搜尋成功，即函式值下降(上升)，下一步仍可沿該方向搜尋，而且可以大步向前搜尋。其作法是：從某點t出發，步長取為λ，若f(t+λ)<(>)f(t)，則搜尋成功，下一步取步長為2λ;如果第n步的步長為nλ，並搜尋成功，下一步取步長為2nλ，若在第k次疊代，沿某方向搜尋失敗，即函式值上升(下降)，則應退回原地，下一步沿相反方向，即向後小步搜尋.其作法是：若f(t+λ)≥(≤)f(t)，則搜尋失敗，退回原來點並且再後退λ/4，若第n步步長為nλ，搜尋失敗，則退回到t後，還要後退nλ/4.直到最後搜尋步長小於給定的小正數，則停止搜尋，得到近似最優點，這裡2λ，λ/4都是按經驗選取的。
基本介紹
- 中文名：成功失敗法
- 外文名：success-failure method
- 別稱：進退法、倍增半減法
- 所屬學科：數學
- 簡介：一種搜尋方法
基本介紹,算法思想,算法步驟,例題解析,
基本介紹
考察一元函式極小化問題
確定一元函式極值點的數值方法，也即單變數尋優，通常稱為一維搜尋。在最最佳化方法中，一維搜尋雖然簡單，但卻重要，因為多維最最佳化問題的求解一般都伴隨著一系列的一維搜尋。
算法思想
在進行一維搜尋的時候需要確定搜尋區間，也就是包含該問題最優解的一個閉區間，然後在此區間內進行搜尋求解。
定義1 若存在
，使得
在
上嚴格遞減，在
上嚴格遞增，則稱
是的下單峰區間，是上的下單峰函式。
顯然，下單峰函式是嚴格凸且有內極小點的函式。
確定下單峰搜尋區間的一個簡單方法就是所謂的成功-失敗法，該方法不要求函式可微，其基本思想是從一初始點出發，按一定步長尋找目標函式值更優的點，一個方向失敗就退回來，向相反的方向尋找，因此，這是一種試探法。
算法步驟
設初始點為
，初始步長
，若
，則下一步從
出發，加大步長，。繼續向前搜尋，否則反向尋找。算法的具體步驟如下。1
第一步：選取初始值：給定初始步長，初始點，
，及
。
第二步：
。
第三步：
。
第四步：比較目標函式值：若
，則轉第五步；否則，轉第六步。
第五步：加大搜尋步長：
，轉第三步。
第六步：判定精度：若
。則轉第七步；否則，轉第八步。
第七步：確定最優解：
。
第八步：反向搜尋：
，轉第三步。
例題解析
【例1】求函式
在
內的近似極小點，
。
解 顯然是下單峰函式，取
按成功一失敗法的步驟進行疊代：
第一次：
比較得到
。
第二次：取
有
第三次：
，有
後續的疊代結果見表1。
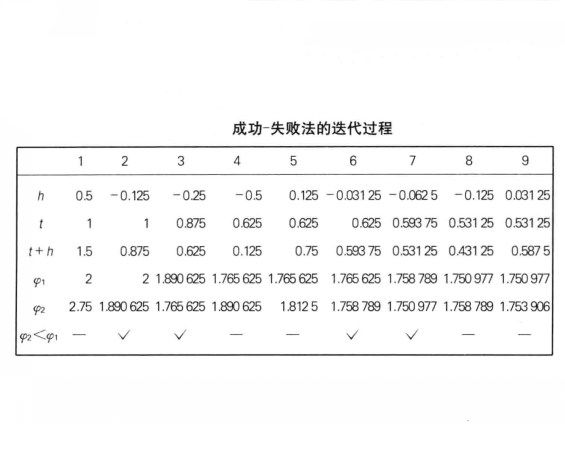
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
h | 0.5 | -0.125 | -0.25 | 一0.5 | 0.125 | -0.031 25 | -0.062 5 | -0.125 | 0.031 25 |
x | 1 | 1 | 0.875 | 0.625 | 0.625 | 0.625 | 0.59375 | 0.531 25 | 0.531 25 |
x+h | 1.5 | 0.875 | 0.625 | 0.125 | 0.75 | 0.59375 | 0.531 25 | 0.431 25 | 0.587 5 |
f1 | 2 | 2 | 1.890625 | 1.765625 | 1.765625 | 1.765625 | 1.758789 | 1.750977 | 1.750977 |
f2 | 2.75 | 1.890625 | 1.765625 | 1.890 625 | 1.812 5 | 1.7587897 | 1.750977 | 1.758789 | 1.753906 |
f2<f1 | —— | √ | √ | —— | —— | √ | √ | —— | —— |
第九次疊代後，，並且，故，
成功-失敗法的優點是起步簡單，缺點是不易識別最優解，並且在最優解附近收斂較慢。實際求解中，可以套用該方法將搜尋區間縮小到一定程度後，停止疊代，把原問題轉化為一個搜尋區間較小的最佳化問題，然後，再套用其他最佳化方法進行求解。
