基本介紹
- 中文名：黃金分割搜尋
- 外文名：Golden-section search
- 學科：數學、計算機科學
- 性質：名詞
- 特點：黃金分割
- 提出者：Kiefer
基本概念,點的選擇,
基本概念
這裡討論的是在一個單峰函式搜尋一個最小值（搜尋一個最大值也一樣），與找零不同，兩個具有相反符號的求值函式足以包括一個根。當搜尋最小值時，需要三個值。黃金分割搜尋是逐步縮小定位最小值的有效方式。關鍵是要觀察，無論有多少點已經被賦值，最小值在由與目前賦值最小的點相鄰的兩點所界定的區間內。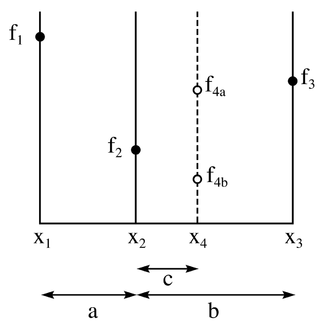
上圖表示了算法中找最小值的一個步驟。f(x)的函式值位於垂直坐標軸上,參數x位於水平坐標軸。已經有三個位於函式f(x)上的點的值被計算出來。: x1, x2, 和x3。可見f2小於 f1和f3, 所以很明顯的，最小值處於x1和x3之間。
接下來的步驟是通過計算函式位於另一個點x4的值。在最大的區間選擇x4會更有效率，例如：x2和x3之間。從圖中我們可以看出，如果函式的值落在f4a的話，最小值落於x1和x4之間，並且新的一組點將會是x1和x2和x4。然而如果函式的值為f4b的話，新的一組點將會是x2和x4和x3。因此，無論是哪種情況，我們都可以建立一個新的更狹窄的區間，用於搜尋函式的最小值。
點的選擇
由圖可知，新的區間會介於X1和X4，長度為a+c，或者介於X2和X3，長度為b。黃金分割搜尋要求這些區間是相等的。若不是如此，較寬的區間會被使用很多次，降低了收斂率。為了確保b=a+c，算法應確保X4=X1-X2+X3。
然而X2的確定仍是一個問題。我們避免了X2非常接近X1或者X3的情況，確保了每一次疊代區間寬度會縮小同樣的比例。
為了確保計算f(X4)後的值與之間的成比例，假設f(X4)的值為f4a，且我們新的一組點為X1,X2和X4，則必須使：
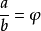
而φ就是黃金比例：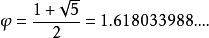
這就是這個算法被成為黃金分割搜尋的原因。
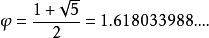
終止條件
由於平滑的函式是平穩的（它們的一階導數接近於零）接近於最小值，所以必須注意不要太高的定位精度，在書<數值分析C語言》中終止條件基於測試X4，X1，X2，X3之間的差距，在相對精度範圍內。
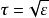
算法
算法包括疊代和遞歸。如下：
'''pythonprogram for golden section search'''
gr =(math.sqrt(5) + 1) / 2
def gss(f, a, b,tol=1e-5):
'''
golden section search
to find the minimum of f on [a,b]
f: a strictly unimodal function on [a,b]
example:
>>> f = lambda x: (x-2)**2
>>> x = gss(f, 1, 5)
>>> x
2.000009644875678
'''
c = b - (b - a) / gr
d = a + (b - a) / gr
while abs(c - d) > tol:
if f(c) < f(d):
b = d
else:
a = c
# we recompute both c and d here toavoid loss of precision which may lead to incorrect results or infinite loop
c = b - (b - a) / gr
d = a + (b - a) / gr
return (b + a) / 2
public static double PHI = (1 +Math.sqrt(5)) / 2; // 0.618...
public static double RESPHI = 2 - PHI; // 0.382...
/**
* Golden section search.
*
* @param x1The left bound of current bounds.
* @param x2An interior point between (x1, x3).
* @param x3The right bound of current bounds.
* @param tau The error tolerance to judgethe convergence, recommended value is e^0.5, where e is is the requiredabsolute precision of f(x).
*/
public double goldenSectionSearch(doublex1, double x2, double x3, double tau) {
double x4;
if (x3 - x2 > x2 - x1) { // b > a，右半區間長度較大
x4 = x2 + RESPHI * (x3 - x2); // x4安插在右半區間
} else {// b <= a，左半區間長度較大
x4 = x2 - RESPHI * (x2 - x1); // x4安插在左半區間
}
if (Math.abs(x3 - x1) < tau *(Math.abs(x2) + Math.abs(x4))) { // 判斷是否達到收斂條件
return (x3 + x1) / 2; // 達到收斂條件，取區間長度的一半作為極小值點輸出
}
assert (function.func(x4) !=function.func(x2));
/* 未達到收斂條件，繼續搜尋 */
if (function.func(x4) <function.func(x2)) { // x4點的函式值如圖中f4b所示時
if (x3 - x2 > x2 - x1) { // b > a，右半區間長度較大
return goldenSectionSearch(x2, x4, x3,tau); // 以x2，x4，x3作為新三點，繼續搜尋
} else {// b <= a，左半區間長度較大
return goldenSectionSearch(x1, x4, x2,tau); // 以x1，x4，x2作為新三點，繼續搜尋
}
} else {// x4點的函式值如圖中f4a所示時
if (x3 - x2 > x2 - x1) { // b > a，右半區間長度較大
return goldenSectionSearch(x1, x2, x4,tau); // 以x1，x2，x4作為新三點，繼續搜尋
} else {// b <= a，左半區間長度較大
return goldenSectionSearch(x4, x2, x3,tau); // 以x4，x2，x3作為新三點，繼續搜尋
}
}
}
斐波那契搜尋
斐波那契數列，又稱黃金分割數列，指的是這樣一個數列：1、1、2、3、5、8、13、21、····，在數學上，斐波那契被遞歸方法如下定義：F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）。該數列越往後相鄰的兩個數的比值越趨向於黃金比例值（0.618）。
斐波那契查找就是在二分查找的基礎上根據斐波那契數列進行分割的。在斐波那契數列找一個等於略大於查找表中元素個數的數F[n]，將原查找表擴展為長度為F[n](如果要補充元素，則補充重複最後一個元素，直到滿足F[n]個元素)，完成後進行斐波那契分割，即F[n]個元素分割為前半部分F[n-1]個元素，後半部分F[n-2]個元素，找出要查找的元素在那一部分並遞歸，直到找到。
斐波那契查找的時間複雜度還是O(log 2 n )，但是與折半查找相比，斐波那契查找的優點是它只涉及加法和減法運算，而不用除法，而除法比加減法要占用更多的時間，因此，斐波那契查找的運行時間理論上比折半查找小，但是還是得視具體情況而定。
對於斐波那契數列：1、1、2、3、5、8、13、21、34、55、89……（也可以從0開始），前後兩個數字的比值隨著數列的增加，越來越接近黃金比值0.618。比如這裡的89，把它想像成整個有序表的元素個數，而89是由前面的兩個斐波那契數34和55相加之後的和，也就是說把元素個數為89的有序表分成由前55個數據元素組成的前半段和由後34個數據元素組成的後半段，那么前半段元素個數和整個有序表長度的比值就接近黃金比值0.618，假如要查找的元素在前半段，那么繼續按照斐波那契數列來看，55 = 34 + 21，所以繼續把前半段分成前34個數據元素的前半段和後21個元素的後半段，繼續查找，如此反覆，直到查找成功或失敗，這樣就把斐波那契數列套用到查找算法中了。
