卡爾曼濾波

卡爾曼濾波（Kalman filtering）一種利用線性系統狀態方程，通過系統輸入輸出觀測數據，對系統狀態進行最優估計的算法。由於觀測數據中包括系統中的噪聲和干擾的影響，所以最優估計也可看作是濾波過程。

斯坦利·施密特(Stanley Schmidt)首次實現了卡爾曼濾波器。卡爾曼在NASA埃姆斯研究中心訪問時，發現他的方法對於解決阿波羅計畫的軌道預測很有用，後來阿波羅飛船的導航電腦使用了這種濾波器。 關於這種濾波器的論文由Swerling (1958), Kalman (1960)與 Kalman and Bucy (1961)發表。

數據濾波是去除噪聲還原真實數據的一種數據處理技術，Kalman濾波在測量方差已知的情況下能夠從一系列存在測量噪聲的數據中，估計動態系統的狀態。由於它便於計算機編程實現，並能夠對現場採集的數據進行實時的更新和處理，Kalman濾波是目前套用最為廣泛的濾波方法，在通信，導航，制導與控制等多領域得到了較好的套用。

基本介紹

• 中文名：卡爾曼濾波器，Kalman濾波，卡曼濾波
• 外文名： KALMAN FILTER
• 表達式：X(k)=A X(k-1)+B U(k)+W(k)
• 提出者：斯坦利·施密特
• 提出時間：1958
• 套用學科：天文，宇航，氣象
• 適用領域範圍：雷達跟蹤去噪聲
• 適用領域範圍：控制、制導、導航、通訊等現代工程

背景

斯坦利·施密特(Stanley Schmidt)首次實現了卡爾曼濾波器。卡爾曼在NASA埃姆斯研究中心訪問時,發現他的方法對於解決阿波羅計畫的軌道預測很有用,後來阿波羅飛船的導航電腦使用了這種濾波器。關於這種濾波器的論文由Swerling (1958), Kalman (1960)與 Kalman and Bucy (1961)發表。

定義

傳統的濾波方法，只能是在有用信號與噪聲具有不同頻帶的條件下才能實現．20世紀40年代，N．維納和A．H．柯爾莫哥羅夫把信號和噪聲的統計性質引進了濾波理論，在假設信號和噪聲都是平穩過程的條件下，利用最最佳化方法對信號真值進行估計，達到濾波目的，從而在概念上與傳統的濾波方法聯繫起來，被稱為維納濾波。這種方法要求信號和噪聲都必須是以平穩過程為條件。60年代初，卡爾曼(R．E．Kalman)和布塞(R． S．Bucy)發表了一篇重要的論文《線性濾波和預測 理論的新成果》，提出了一種新的線性濾波和預測理由論，被稱之為卡爾曼濾波。特點是線上性狀態空間表示的基礎上對有噪聲的輸入和觀測信號進行處理，求取系統狀態或真實信號。

這種理論是在時間域上來表述的，基本的概念是：線上性系統的狀態空間表示基礎上，從輸出和輸入觀測數據求系統狀態的最優估計。這裡所說的系統狀態，是總結系統所有過去的輸入和擾動對系統的作用的最小參數的集合，知道了系統的狀態就能夠與未來的輸入與系統的擾動一起確定系統的整個行為。

卡爾曼濾波不要求信號和噪聲都是平穩過程的假設條件。對於每個時刻的系統擾動和觀測誤差（即噪聲），只要對它們的統計性質作某些適當的假定，通過對含有噪聲的觀測信號進行處理，就能在平均的意義上，求得誤差為最小的真實信號的估計值。因此，自從卡爾曼濾波理論問世以來，在通信系統、電力系統、航空航天、環境污染控制、工業控制、雷達信號處理等許多部門都得到了套用，取得了許多成功套用的成果。例如在圖像處理方面，套用卡爾曼濾波對由於某些噪聲影響而造成模糊的圖像進行復原。在對噪聲作了某些統計性質的假定後，就可以用卡爾曼的算法以遞推的方式從模糊圖像中得到均方差最小的真實圖像，使模糊的圖像得到復原。

性質

①卡爾曼濾波是一個算法，它適用於線性、離散和有限維系統。每一個有外部變數的自回歸移動平均系統(ARMAX)或可用有理傳遞函式表示的系統都可以轉換成用狀態空間表示的系統，從而能用卡爾曼濾波進行計算。

②任何一組觀測數據都無助於消除x(t)的確定性。增益K(t)也同樣地與觀測數據無關。

③當觀測數據和狀態聯合服從高斯分布時用卡爾曼遞歸公式計算得到的是高斯隨機變數的條件均值和條件方差，從而卡爾曼濾波公式給出了計算狀態的條件機率密度的更新過程線性最小方差估計，也就是最小方差估計。

形式

卡爾曼濾波已經有很多不同的實現，卡爾曼最初提出的形式一般稱為簡單卡爾曼濾波器。除此以外，還有施密特擴展濾波器、信息濾波器以及很多Bierman, Thornton 開發的平方根濾波器的變種。最常見的卡爾曼濾波器是鎖相環，它在收音機、計算機和幾乎任何視頻或通訊設備中廣泛存在。

實例

卡爾曼濾波的一個典型實例是從一組有限的，對物體位置的，包含噪聲的觀察序列中預測出物體的坐標位置及速度。在很多工程套用(雷達、計算機視覺)中都可以找到它的身影。同時，卡爾曼濾波也是控制理論以及控制系統工程中的一個重要話題。

套用

比如，在雷達中，人們感興趣的是跟蹤目標，但目標的位置、速度、加速度的測量值往往在任何時候都有噪聲。卡爾曼濾波利用目標的動態信息,設法去掉噪聲的影響，得到一個關於目標位置的好的估計。這個估計可以是對當前目標位置的估計(濾波)，也可以是對於將來位置的估計(預測)，也可以是對過去位置的估計(插值或平滑)。

擴展卡爾曼濾波（EXTEND KALMAN FILTER, EKF）

擴展卡爾曼濾波器

是由kalman filter考慮時間非線性的動態系統，常套用於目標跟蹤系統。

狀態估計

狀態估計

狀態估計是卡爾曼濾波的重要組成部分。一般來說，根據觀測數據對隨機量進行定量推斷就是估計問題，特別是對動態行為的狀態估計，它能實現實時運行狀態的估計和預測功能。比如對飛行器狀態估計。狀態估計對於了解和控制一個系統具有重要意義，所套用的方法屬於統計學中的估計理論。最常用的是最小二乘估計，線性最小方差估計、最小方差估計、遞推最小二乘估計等。其他如風險準則的貝葉斯估計、最大似然估計、隨機逼近等方法也都有套用。

狀態量

受噪聲干擾的狀態量是個隨機量，不可能測得精確值，但可對它進行一系列觀測，並依據一組觀測值，按某種統計觀點對它進行估計。使估計值儘可能準確地接近真實值，這就是最優估計。真實值與估計值之差稱為估計誤差。若估計值的數學期望與真實值相等，這種估計稱為無偏估計。卡爾曼提出的遞推最優估計理論，採用狀態空間描述法，在算法採用遞推形式，卡爾曼濾波能處理多維和非平穩的隨機過程。

理論

卡爾曼濾波理論的提出，克服了威納濾波理論的局限性使其在工程上得到了廣泛的套用，尤其在控制、制導、導航、通訊等現代工程方面。

MATLAB程式

MATLAB

N=200;

w(1)=0;

w=randn(1,N)

x(1)=0;

a=1;

for k=2:N;

x(k)=a*x(k-1)+w(k-1);

end

V=randn(1,N);

q1=std(V);

Rvv=q1.^2;

q2=std(x);

Rxx=q2.^2;

q3=std(w);

Rww=q3.^2;

c=0.2;

Y=c*x+V;

p(1)=0;

s(1)=0;

for t=2:N;

p1(t)=a.^2*p(t-1)+Rww;

b(t)=c*p1(t)/(c.^2*p1(t)+Rvv);

s(t)=a*s(t-1)+b(t)*(Y(t)-a*c*s(t-1));

p(t)=p1(t)-c*b(t)*p1(t);

end

t=1:N;

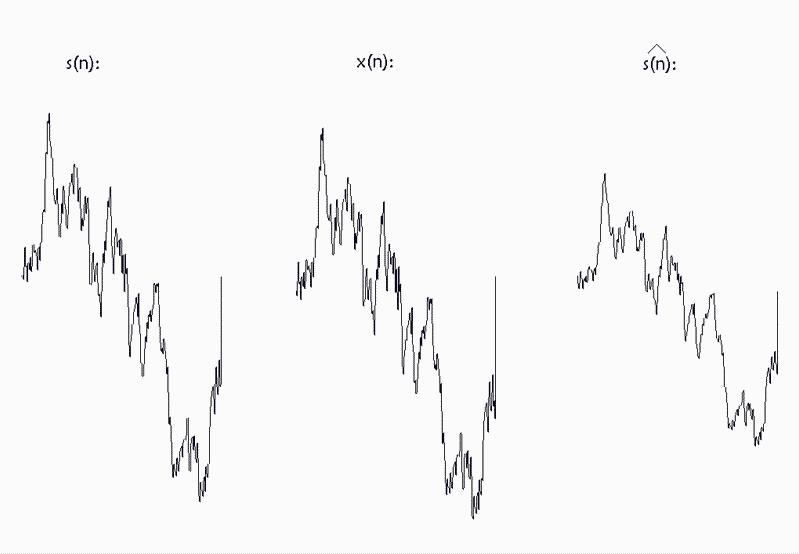
plot(t,s,'r',t,Y,'g',t,x,'b');

function [x, V, VV, loglik] = kalman_filter(y, A, C, Q, R, init_x, init_V, varargin)

% Kalman filter.

% [x, V, VV, loglik] = kalman_filter(y, A, C, Q, R, init_x, init_V, ...)

%

% INPUTS:

% y(:,t) - the observation at time t

% A - the system matrix

% C - the observation matrix

% Q - the system covariance

% R - the observation covariance

% init_x - the initial state (column) vector

% init_V - the initial state covariance

%

% OPTIONAL INPUTS (string/value pairs [default in brackets])

% 'model' - model(t)=m means use params from model m at time t [ones(1,T) ]

% In this case, all the above matrices take an additional final dimension,

% i.e., A(:,:,m), C(:,:,m), Q(:,:,m), R(:,:,m).

% However, init_x and init_V are independent of model(1).

% 'u' - u(:,t) the control signal at time t [ [] ]

% 'B' - B(:,:,m) the input regression matrix for model m

%

% OUTPUTS (where X is the hidden state being estimated)

% x(:,t) = E[X(:,t) | y(:,1:t)]

% V(:,:,t) = Cov[X(:,t) | y(:,1:t)]

% VV(:,:,t) = Cov[X(:,t), X(:,t-1) | y(:,1:t)] t >= 2

% loglik = sum{t=1}^T log P(y(:,t))

%

% If an input signal is specified, we also condition on it:

% e.g., x(:,t) = E[X(:,t) | y(:,1:t), u(:, 1:t)]

% If a model sequence is specified, we also condition on it:

% e.g., x(:,t) = E[X(:,t) | y(:,1:t), u(:, 1:t), m(1:t)]

[os T] = size(y);

ss = size(A,1); % size of state space

% set default params

model = ones(1,T);

u = [];

B = [];

ndx = [];

args = varargin;

nargs = length(args);

for i=1:2:nargs

switch args

case 'model', model = args{i+1};

case 'u', u = args{i+1};

case 'B', B = args{i+1};

case 'ndx', ndx = args{i+1};

otherwise, error(['unrecognized argument ' args])

end

end

x = zeros(ss, T);

V = zeros(ss, ss, T);

VV = zeros(ss, ss, T);

loglik = 0;

for t=1:T

m = model(t);

if t==1

%prevx = init_x(:,m);

%prevV = init_V(:,:,m);

prevx = init_x;

prevV = init_V;

initial = 1;

else

prevx = x(:,t-1);

prevV = V(:,:,t-1);

initial = 0;

end

if isempty(u)

[x(:,t), V(:,:,t), LL, VV(:,:,t)] = ...

kalman_update(A(:,:,m), C(:,:,m), Q(:,:,m), R(:,:,m), y(:,t), prevx, prevV, 'initial', initial);

else

if isempty(ndx)

[x(:,t), V(:,:,t), LL, VV(:,:,t)] = ...

kalman_update(A(:,:,m), C(:,:,m), Q(:,:,m), R(:,:,m), y(:,t), prevx, prevV, ...

'initial', initial, 'u', u(:,t), 'B', B(:,:,m));

else

i = ndx;

% copy over all elements; only some will get updated

x(:,t) = prevx;

prevP = inv(prevV);

prevPsmall = prevP(i,i);

prevVsmall = inv(prevPsmall);

[x(i,t), smallV, LL, VV(i,i,t)] = ...

kalman_update(A(i,i,m), C(:,i,m), Q(i,i,m), R(:,:,m), y(:,t), prevx(i), prevVsmall, ...

'initial', initial, 'u', u(:,t), 'B', B(i,:,m));

smallP = inv(smallV);

prevP(i,i) = smallP;

V(:,:,t) = inv(prevP);

end

end

loglik = loglik + LL;

end

另一個例子：

Z=(1:100); %觀測值

noise=randn(1,100); %方差為1的高斯噪聲

Z=Z+noise;

X=[0;0]; %狀態

P=[10;01]; %狀態協方差矩陣

F=[11;01]; %狀態轉移矩陣

Q=[0.0001,0;00.0001]; %狀態轉移協方差矩陣

H=[10]; %觀測矩陣

R=1; %觀測噪聲方差

figure;

hold on;

fori=1:100

X_ = F*X;

P_ = F*P*F'+Q;

K = P_*H'/(H*P_*H'+R);

X = X_+K*(Z(i)-H*X_);

P = (eye(2)-K*H)*P_;

plot(X(1), X(2)); %畫點，橫軸表示位置，縱軸表示速度

end

通俗解釋

簡單來說，卡爾曼濾波器是一個“optimal recursive data processing algorithm（最最佳化自回歸數據處理算法）”。對於解決很大部分的問題，他是最優，效率最高甚至是最有用的。他的廣泛套用已經超過30年，包括機器人導航，控制，感測器數據融合甚至在軍事方面的雷達系統以及飛彈追蹤等等。近來更被套用於計算機圖像處理，例如頭臉識別，圖像分割，圖像邊緣檢測等等。

卡爾曼濾波器的介紹 ：

為了可以更加容易的理解卡爾曼濾波器，這裡會套用形象的描述方法來講解，而不是像大多數參考書那樣羅列一大堆的數學公式和數學符號。但是，他的5條公式是其核心內容。結合現代的計算機，其實卡爾曼的程式相當的簡單，只要你理解了他的那5條公式。

在介紹他的5條公式之前，先讓我們來根據下面的例子一步一步的探索。

假設我們要研究的對象是一個房間的溫度。根據你的經驗判斷，這個房間的溫度是恆定的，也就是下一分鐘的溫度等於現在這一分鐘的溫度（假設我們用一分鐘來做時間單位）。假設你對你的經驗不是100%的相信，可能會有上下偏差幾度。我們把這些偏差看成是高斯白噪聲（White Gaussian Noise），也就是這些偏差跟前後時間是沒有關係的而且符合高斯分布（Gaussian Distribution）。另外，我們在房間裡放一個溫度計，但是這個溫度計也不準確的，測量值會比實際值偏差。我們也把這些偏差看成是高斯白噪聲。

好了，現在對於某一分鐘我們有兩個有關於該房間的溫度值：你根據經驗的預測值（系統的預測值）和溫度計的值（測量值）。下面我們要用這兩個值結合他們各自的噪聲來估算出房間的實際溫度值。

假如我們要估算k時刻的實際溫度值。首先你要根據k-1時刻的溫度值，來預測k時刻的溫度。因為你相信溫度是恆定的，所以你會得到k時刻的溫度預測值是跟k-1時刻一樣的，假設是23度，同時該值的高斯噪聲的偏差是5度（5是這樣得到的：如果k-1時刻估算出的最優溫度值的偏差是3，你對自己預測的不確定度是4度，他們平方相加再開方，就是5）。然後，你從溫度計那裡得到了k時刻的溫度值，假設是25度，同時該值的偏差是4度。

由於我們用於估算k時刻的實際溫度有兩個溫度值，分別是23度和25度。究竟實際溫度是多少呢？相信自己還是相信溫度計呢？究竟相信誰多一點，我們可以用他們的協方差(covariance)來判斷。因為Kg=5^2/(5^2+4^2)，所以Kg=0.61，我們可以估算出k時刻的實際溫度值是：23+0.61*(25-23)=24.22度。可以看出，因為溫度計的協方差(covariance)比較小（比較相信溫度計），所以估算出的最優溫度值偏向溫度計的值。

現在我們已經得到k時刻的最優溫度值了，下一步就是要進入k+1時刻，進行新的最優估算。到現在為止，好像還沒看到什麼自回歸的東西出現。對了，在進入k+1時刻之前，我們還要算出k時刻那個最優值（24.22度）的偏差。算法如下：((1-Kg)*5^2)^0.5=3.12。這裡的5就是上面的k時刻你預測的那個23度溫度值的偏差，得出的3.12就是進入k+1時刻以後k時刻估算出的最優溫度值的偏差（對應於上面的3）。

就是這樣，卡爾曼濾波器就不斷的把協方差(covariance)遞歸，從而估算出最優的溫度值。他運行的很快，而且它只保留了上一時刻的協方差(covariance)。上面的Kg，就是卡爾曼增益（Kalman Gain）。他可以隨不同的時刻而改變他自己的值，是不是很神奇！

下面就要言歸正傳，討論真正工程系統上的卡爾曼。

卡爾曼濾波器算法 ：

在這一部分，我們就來描述源於Dr Kalman 的卡爾曼濾波器。下面的描述，會涉及一些基本的概念知識，包括機率（Probability），隨機變數（Random Variable），高斯或正態分配（Gaussian Distribution）還有State-space Model等等。但對於卡爾曼濾波器的詳細證明，這裡不能一一描述。

首先，我們先要引入一個離散控制過程的系統。該系統可用一個線性隨機微分方程（Linear Stochastic Difference equation）來描述：

X(k)=A X(k-1)+B U(k)+W(k)

再加上系統的測量值：

Z(k)=H X(k)+V(k)

上兩式子中，X(k)是k時刻的系統狀態，U(k)是k時刻對系統的控制量。A和B是系統參數，對於多模型系統，他們為矩陣。Z(k)是k時刻的測量值，H是測量系統的參數，對於多測量系統，H為矩陣。W(k)和V(k)分別表示過程和測量的噪聲。他們被假設成高斯白噪聲(White Gaussian Noise)，他們的協方差(covariance)分別是Q，R（這裡我們假設他們不隨系統狀態變化而變化）。

對於滿足上面的條件(線性隨機微分系統，過程和測量都是高斯白噪聲)，卡爾曼濾波器是最優的信息處理器。下面我們結合他們的協方差來估算系統的最最佳化輸出（類似上一節那個溫度的例子）。

首先我們要利用系統的過程模型，來預測下一狀態的系統。假設現在的系統狀態是k，根據系統的模型，可以基於系統的上一狀態而預測出現在狀態：

X(k|k-1)=A X(k-1|k-1)+B U(k) ……….. (1)

式(1)中，X(k|k-1)是利用上一狀態預測的結果，X(k-1|k-1)是上一狀態最優的結果，U(k)為現在狀態的控制量，如果沒有控制量，它可以為0。

到現在為止，我們的系統結果已經更新了，可是，對應於X(k|k-1)的協方差還沒更新。我們用P表示協方差(covariance)：

P(k|k-1)=A P(k-1|k-1) A’+Q ……… (2)

式(2)中，P(k|k-1)是X(k|k-1)對應的協方差，P(k-1|k-1)是X(k-1|k-1)對應的協方差，A’表示A的轉置矩陣，Q是系統過程的協方差。式子1，2就是卡爾曼濾波器5個公式當中的前兩個，也就是對系統的預測。

現在我們有了現在狀態的預測結果，然後我們再收集現在狀態的測量值。結合預測值和測量值，我們可以得到現在狀態(k)的最最佳化估算值X(k|k)：

X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)

其中Kg為卡爾曼增益(Kalman Gain)：

Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) ……… (4)

到現在為止，我們已經得到了k狀態下最優的估算值X(k|k)。但是為了要令卡爾曼濾波器不斷的運行下去直到系統過程結束，我們還要更新k狀態下X(k|k)的協方差：

P(k|k)=（I-Kg(k) H）P(k|k-1) ……… (5)

其中I 為1的矩陣，對於單模型單測量，I=1。當系統進入k+1狀態時，P(k|k)就是式子(2)的P(k-1|k-1)。這樣，算法就可以自回歸的運算下去。

卡爾曼濾波器的原理基本描述了，式子1，2，3，4和5就是他的5 個基本公式。根據這5個公式，可以很容易用計算機編程實現。

在上面的例子中，過程誤差和測量誤差設定為4是為了討論的方便。實際中，溫度的變化速度以及溫度計的測量誤差都沒有這么大。

假設如下一個系統：

• 房間內連續兩個時刻溫度差值的標準差為0.02度
  
• 溫度計的測量值誤差的標準差為0.5度
  
• 房間溫度的真實值為24度
  
• 對溫度的初始估計值為23.5度，誤差的方差為1
  

MatLab仿真的代碼如下：

% Kalman filter example of temperature measurement in Matlab

% This M code is modified from Xuchen Yao's matlab on 2013/4/18

%房間當前溫度真實值為24度，認為下一時刻與當前時刻溫度相同，誤差為0.02度（即認為連續的兩個時刻最多變化0.02度）。

%溫度計的測量誤差為0.5度。

%開始時，房間溫度的估計為23.5度，誤差為1度。

% Kalman filter example demo in Matlab

% This M code is modified from Andrew D. Straw's Python

% implementation of Kalman filter algorithm.

% The original code is from the link in references

% Below is the Python version's comments:

% Kalman filter example demo in Python

% A Python implementation of the example given in pages 11-15 of "An

% Introduction to the Kalman Filter" by Greg Welch and Gary Bishop,

% University of North Carolina at Chapel Hill, Department of Computer

% Science, TR 95-041,

% by Andrew D. Straw

% by Xuchen Yao

% by Lin Wu

clear all;

close all;

% intial parameters

n_iter = 100; %計算連續n_iter個時刻

sz = [n_iter, 1]; % size of array. n_iter行，1列

x = 24; % 溫度的真實值

Q = 4e-4; % 過程方差， 反應連續兩個時刻溫度方差。更改查看效果

R = 0.25; % 測量方差，反應溫度計的測量精度。更改查看效果

z = x + sqrt(R)*randn(sz); % z是溫度計的測量結果，在真實值的基礎上加上了方差為0.25的高斯噪聲。

% 對數組進行初始化

xhat=zeros(sz); % 對溫度的後驗估計。即在k時刻，結合溫度計當前測量值與k-1時刻先驗估計，得到的最終估計值

P=zeros(sz); % 後驗估計的方差

xhatminus=zeros(sz); % 溫度的先驗估計。即在k-1時刻，對k時刻溫度做出的估計

Pminus=zeros(sz); % 先驗估計的方差

K=zeros(sz); % 卡爾曼增益，反應了溫度計測量結果與過程模型（即當前時刻與下一時刻溫度相同這一模型）的可信程度

% intial guesses

xhat(1) = 23.5; %溫度初始估計值為23.5度

P(1) =1; %誤差方差為1

for k = 2:n_iter

% 時間更新（預測）

xhatminus(k) = xhat(k-1); %用上一時刻的最優估計值來作為對當前時刻的溫度的預測

Pminus(k) = P(k-1)+Q; %預測的方差為上一時刻溫度最優估計值的方差與過程方差之和

% 測量更新（校正）

K(k) = Pminus(k)/( Pminus(k)+R ); %計算卡爾曼增益

xhat(k) = xhatminus(k)+K(k)*(z(k)-xhatminus(k)); %結合當前時刻溫度計的測量值，對上一時刻的預測進行校正，得到校正後的最優估計。該估計具有最小均方差

P(k) = (1-K(k))*Pminus(k); %計算最終估計值的方差

end

FontSize=14;

LineWidth=3;

figure();

plot(z,'k+'); %畫出溫度計的測量值

估計的誤差的方差

hold on;

plot(xhat,'b-','LineWidth',LineWidth) %畫出最優估計值

hold on;

plot(x*ones(sz),'g-','LineWidth',LineWidth); %畫出真實值

legend('溫度計的測量結果', '後驗估計', '真實值');

xl=xlabel('時間(分鐘)');

yl=ylabel('溫度');

set(xl,'fontsize',FontSize);

set(yl,'fontsize',FontSize);

hold off;

set(gca,'FontSize',FontSize);

figure();

valid_iter = [2:n_iter]; % Pminus not valid at step 1

plot(valid_iter,P([valid_iter]),'LineWidth',LineWidth); %畫出最優估計值的方差

legend('後驗估計的誤差估計');

xl=xlabel('時間(分鐘)');

yl=ylabel('℃^2');

set(xl,'fontsize',FontSize);

set(yl,'fontsize',FontSize);

set(gca,'FontSize',FontSize);

概念

最佳線性濾波理論起源於40年代美國科學家Wiener和前蘇聯科學家Kолмогоров等人的研究工作，後人統稱為維納濾波理論。從理論上說，維納濾波的最大缺點是必須用到無限過去的數據，不適用於實時處理。為了克服這一缺點，60年代Kalman把狀態空間模型引入濾波理論，並導出了一套遞推估計算法，後人稱之為卡爾曼濾波理論。卡爾曼濾波是以最小均方誤差為估計的最佳準則，來尋求一套遞推估計的算法，其基本思想是：採用信號與噪聲的狀態空間模型，利用前一時刻的估計值和現時刻的觀測值來更新對狀態變數的估計，求出現時刻的估計值。它適合於實時處理和計算機運算。

卡爾曼濾波的結果

卡爾曼濾波的實質是由量測值重構系統的狀態向量。它以“預測—實測—修正”的順序遞推，根據系統的量測值來消除隨機干擾，再現系統的狀態，或根據系統的量測值從被污染的系統中恢復系統的本來面目。