基本介紹
- 中文名:仿射不變數
- 外文名:affine invariant
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
- 簡介:圖形經過仿射變換不改變的量
- 別名:圖形的仿射性質
基本介紹







相關定理和推論
典型例題分析

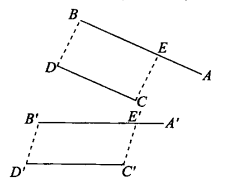




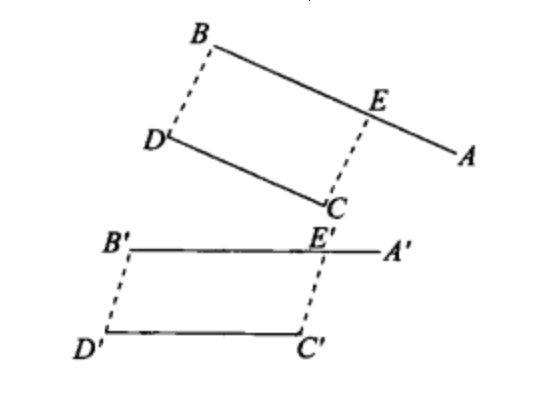













仿射不變數(affine invariant)是仿射變換的一種特徵,指圖形經過任何仿射對應(變換)都不改變的量。共線三點的單比是最基本、最重要的仿射不變數,其他如兩平行的有向線段之比、平行平面(包括同一平面)上兩個封閉圖...
仿射不變性是一個數學名詞,若一個圖形具有某種性質或者某個量,在平行射影下,如果不變,稱這個性質為仿射不變性質,這個量稱為仿射不變數。其性質被稱作仿射不變性。經過仿射對應它們也是不變的。同素性、結合性都是仿射不變性質(也...
本項目提出一種快速魯棒的圖像局部仿射不變特徵提取方法。該方法首先對圖像進行M進制小波變換,根據M進制小波變換係數的能量性質來檢測圖像特徵點;然後以檢測到的穩定特徵點為中心,根據特徵點周圍的局部圖像信息,以矩的形式構造仿射不變...
項目主要研究工作包括:(1) 針對圖像發生仿射變換的情況,構造了Legendre矩的幾何不變數,並將其套用於數字圖像水印;(2) 針對圖像被模糊以及發生幾何變換(旋轉、縮放和平衡)的情況,構造了Zernike矩的模糊以及幾何變換不變數;(3) 構造...
本項目研究有限維空間上凸體間的Banch-Mazur距離(簡記B-M)、凸體非對稱度、體積比等Banach空間局部理論與凸幾何分析中極其重要的一些仿射不變數的基礎性質及相關的幾何不等式。研究內容涉及Banach空間局部理論、現代凸幾何理論、Brunn-...
其他仿射不變數都可以用單比表示。在仿射平面(空間)中,仿射變換的全體構成一個變換群,稱為仿射變換群,簡稱仿射群。並且在擴大的仿射平面(空間)中,它還是保持無窮遠直線(無窮遠平面)不變的一個射影變換群。因此,仿射群是射影群的...
把同一平面內單方面的透視仿射對應,稱為透視仿射變換。有限回的透視仿射變換組成仿射變換。仿射變換的主要性質有:1.二直線的平行性是仿射變換的不變性質。2.三點的簡比是仿射變換的不變數。3.兩條平行線段之比是仿射變換的不變數...
該方法不受矩的維數和階數的限制,可以產生任意形式的相似矩不變數。該方法是第一個基於充要條件的可解的相似矩不變數生成規則,其生成的矩不變數空間是完備和線性獨立的。 給出了一種生成任意維仿射不變數的方法。該方法選取行列式作為...
仿射變換 仿射空間中最重要的變換是仿射變換,它的特徵是將共線的三點變為共線的三點。給定仿射坐標系後,仿射變換有明確的代數表示。仿射變換全體構成的變換群稱為仿射變換群。仿射變換下重要的不變性質和不變數有:共線性、平行性、...
不變數的定義 由幾何學知道,射影變換保持直線、直線與點的結合性以及直線上點列的交比不變,仿射變換除具有以上不變性還保持了直線的平行性,直線上點列的簡比不變。歐氏變換除具有仿射不變性外還保持兩條直線的夾角不變,任意兩點的...
在歐氏平面上添加了一個無窮遠點後,得到一條新的直線,我們將它稱為仿射直線;如果把仿射直線上的有窮點和無窮遠點等同看待而不加區分,則這條直線就稱為射影直線(如圖1)。歐氏直線a上添加一個無窮遠點,記作P,就得到一條仿射...
按照這種方式把M點變換為M’點,它在坐標系O'X’Y’中的坐標為 因為在仿射變換中簡比是不變數,所以 笛卡爾坐標的仿射變換就是這個等式的推廣,因為各軸的度量單位是不同的。在仿射變換中,新得到的坐標系仍是仿射坐標系。
仿射主曲率是數學術語。仿射主曲率,刻畫仿射空間中超曲面彎曲程度的不變數.它是歐氏曲面論中主曲率的仿射類似.設M是n+1維仿射空間中的局部嚴格凸的超曲面,二是位置向量,(u1,uz}...}u}})是局部坐標,Y是仿射法向量場.Y關於u'...
仿射球面(affine hypersurface)是一個重要的超曲面,指仿射空間中仿射法線交於一點或互相平行非退化的超曲面。一個局部嚴格凸的仿射球稱為虛的或拋物型的仿射球面,若它的仿射法線互相平行。概念 仿射球面(affine hypersurface)是一個重要...
單比(simple ratio)亦稱仿射比,又稱簡單比,是仿射幾何中最基本的不變數。若P₁,P₂是有向直線上的兩個定點,P是這直線上的另一點,P分有向線段 為兩個有向線段 和 ,則其數量的比 稱為三點P₁,P₂,P的單比,...
它們不需要斷裂輪廓連線和跟蹤,而且不僅能利用目標的外部輪廓,還能利用目標內部的邊緣,在目標邊緣信息提取出現斷裂、丟失的情況下能夠保持較高的魯棒性,在一定程度上克服了基於輪廓的仿射不變數的不足。
本課題針對非傳統視覺對應點匹配中特有的問題,將從三個方面展開研究:第一,對魚眼圖像之間的對應點匹配,不需要將魚眼圖像轉化為透視圖像,直接採用基於仿射不變數的特徵點檢測和匹配方法,重點研究基於魯棒性統計的匹配方法,同時還將對...
仿射幾何和射影幾何的區別就在於諸如平行這種仿射不變數的概念是前者的恰當主題,而對後者來說卻不是主要概念。然後,通過從各個幾何中抽象出基礎的對稱群,它們之間的關係可以在群的級別重新建立。因為仿射幾何的群是射影幾何的群的子群,...
2 蘇步青論B6zier曲線的仿射不變數 2.1 n次平面Bezier曲線的仿射不變數 2.2 三次平面Bezier曲線的保凸性 2.3 四次平面Bezier曲線的拐點 2.4 幾個具體的例子 3 華宣積論四次、Bezier曲線的拐點和奇點 3.1 四次Bezier曲線的...
另外,當圓拉伸為橢圓,例如把圓的縱坐標變為原來的t(t≠0)倍時,由於單比是仿射變換不變數,所以(1)中BM/AM不變。而k=tk,k=tk,所以有 不變。根據橢圓的第三定義,為定值。而如果M是定點,則kk為定值,所以得到kk為...
簡稱射影群。是一類基本的變換群。即由射影空間中全體射影變換所構成的變換群。例如平面上全體射影變換構成平面上的射影群。空間中全體射影變換構成空間中的射影群。研究在射影群下不變性質與不變數的幾何稱為射影幾何。仿射變換群 簡稱...
例如,平面上的全體仿射變換構成平面上的仿射變換群,它是平面射影變換中以無窮遠直線為絕對形的自同構群。空間中全體仿射變換構成空間的仿射變換群,它是空間射影變換中以無窮遠平面為絕對形的自同構群。研究在仿射群下不變性質與不變數...
例如,平面上的全體仿射變換構成平面上的仿射變換群,它是平面射影變換中以無窮遠直線為絕對形的自同構群。空間中全體仿射變換構成空間的仿射變換群,它是空間射影變換中以無窮遠平面為絕對形的自同構群。研究在仿射群下不變性質與不變數...
在歐氏平面上添加了一個無窮遠點後,得到一條新的直線,我們將它稱為仿射直線;如果把仿射直線上的有窮點和無窮遠點等同看待而不加區分,則這條直線就稱為射影直線(如圖1)。歐氏直線a上添加一個無窮遠點,記作P,就得到一條仿射...
