射影不變數(projective invariant)是射影變換的一種特徵。指圖形經過任何射影對應(變換)都不變的量。射影變換是射影幾何中最重要的幾何變換。這種變換的主要特點是保持結合性。例如，點與直線及點與平面的結合性等。交比是射影幾何中最基本的不變數，其他不變數都可以用交比表示出來。
基本介紹
- 中文名：射影不變數
- 外文名：projective invariant
- 領域：數學
- 學科：射影幾何
- 定義：射影變換的一種特徵
- 例子：交比
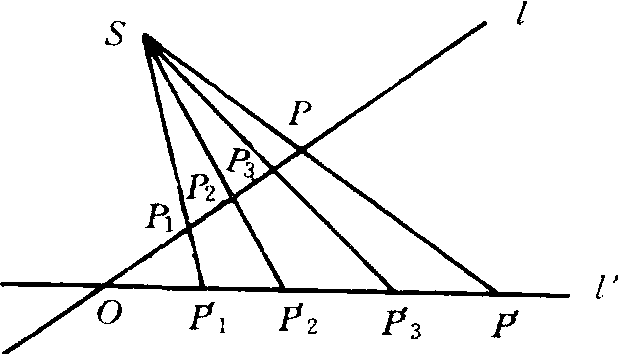
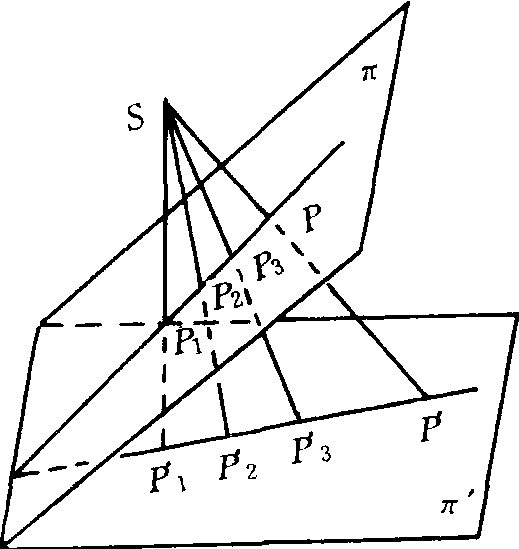
定義,射影幾何,射影變換,交比,
定義
射影不變數(projective invariant)是射影變換的一種特徵。指圖形經過任何射影對應(變換)都不變的量。射影不變數也是一種射影性質。例如，交比就是最基本的射影不變數，同時也是最重要的射影性質。
射影幾何
亦稱投影幾何。幾何學的一個分支。主要研究圖形在射影對應(射影變換)下不變的幾何性質。射影變換是射影幾何中最重要的幾何變換。這種變換的主要特點是保持結合性。例如，點與直線及點與平面的結合性等。交比是射影幾何中最基本的不變數，其他不變數都可以用交比表示出來。
射影幾何的思想，特別是其中的透視投影原理，早在古羅馬時代已為畫家所認識和套用；射影幾何的基本不變數——交比，早已為帕普斯((A).Pappus)所熟知；射影幾何的一些命題也早已為古代幾何學家所得到。然而，射影幾何作為幾何學的一個獨立分支學科卻是在19世紀初期，隨著幾何學的發展以及繪畫與建築的需要而形成和發展起來的。1822年，彭賽列(J.-V.Poncelet)發表了射影幾何的第一部系統著作《論圖形的射影性質》一書。他通過幾何方法引進無窮遠元素，研究了二次曲線和二次曲面的配極理論，並由此導出一般的對偶原理。稍後，施泰納(J.Steiner)研究了利用簡單圖形產生較複雜圖形的方法，並於1832年引進了線素二次曲線概念。1847年，馮·施陶特(K.G.C.von Staudt)通過幾何作圖來建立直線上點的坐標，進而使交比與射影坐標不依賴於任何度量。此外，他還以精巧的方法給出虛元素的幾何解釋。與此同時，運用解析法研究射影幾何也有了長足的發展。首先是默比烏斯(Mo¨bius，A.F.)創立了一種齊次坐標，揭示了對偶原理與配極之間的關係，並於1827年對交比的概念給出了完善的處理。接著，普呂克(J.Plücker)引進了另一種齊次坐標，得到了平面上無窮遠線的方程和無窮遠圓點的坐標。他還引入了線坐標的概念，於是從代數觀點自然就得到對偶原理，並得到一般線曲線的概念。在19世紀前半葉的幾何研究中，綜合法與解析法的爭論非常激烈。一些幾何學家堅持運用綜合法，如彭賽列、施泰納等。綜合法也確實有它獨特的優點，它形象鮮明，使有些問題的論證直接而簡潔。由於他們的努力，使綜合射影幾何形成了一個優美的體系。1882年，帕施(M.Pasch)建立了第一個射影幾何演繹體系。1872年，克萊因((C.)F.Klein)利用變換群的觀點把各種幾何學聯繫起來，他在埃爾朗根綱領中提出了這個觀點，並把幾種經典幾何看做是射影幾何的子幾何，使這些幾何之間的關係變得更加明朗。
射影變換
在歐氏平面上，對於“一組有定方位的一切直線”添加一個點稱為該方位的無窮遠點，此點在該組中的每一直線上，而不在這組以外的直線上；為了區分，以前所見的點稱為有窮點；由於不同方位的直線有不同的無窮遠點，這樣，平面上一切無窮遠點的集合組成一條直線稱為無窮遠直線，以前所見的直線稱為有窮直線；一組平行平面相交於一條無窮遠直線。空間內一切無窮遠點的集合組成一個平面稱為無窮遠平面，以前所見的平面稱為有窮平面。無窮遠點、無窮遠直線、無窮遠平面統稱之為無窮遠元素。
在歐氏平面上添加了一個無窮遠點後，得到一條新的直線，我們將它稱為仿射直線;如果把仿射直線上的有窮點和無窮遠點等同看待而不加區分，則這條直線就稱為射影直線(如圖1)。歐氏直線a上添加一個無窮遠點，記作P∞，就得到一條仿射直線;反過來，如果將射影直線上某一定點認為是無窮遠點，而將其餘點定為有窮點，即得到一條仿射直線，仿射直線上有窮點和無窮遠點不加區分就是一條射影直線，故得射影直線可看作是封閉的，歐氏平面上的圓，常可以作為射影直線的模型。
圖1 射影直線
仿此，在歐氏平面上，添加一條無窮遠直線，記作l∞，即得到一個仿射平面，在仿射平面上有窮、無窮不加區分就是射影平面(二維射影空間)： 反之，如將射影平面內去掉一條直線就轉到歐氏平面了。在歐氏三維空間，添加一個無窮遠平面，記作π∞，即得到仿射空間，仿射空間內有窮、無窮不加區分就是射影空間。在射影空間裡，任何兩條直線、一直線與一個平面至少有一個交點;任何兩個平面必相交於一條直線，任意兩點決定一條直線; 任意不共線的3點必決定一個平面，任意不共線的3個平面必恰有一個交點。由上面的結論可以看出，結合關係是射影平面和射影空間的基本關係。點在直線上與直線通過點有完全的對稱性，也就是使得點和直線在邏輯上取得平等的地位，它們稱為平面上的對偶元素，我們把平面上一個以點和直線構成的圖形，把其中的點和直線互換就得到一個新的圖形稱為已知圖形的對偶圖形，如平面內 “在一直線上一切點的集合” 稱為以該直線為底的點列和平面內 “通過同一點的一切直線的集合”稱為以定點為中心的線束，二者互為對偶圖形。在一個平面上，一切點的集合稱為點場和一切直線的集合稱為線場，點場和線場也是平面對偶圖形; 平面上，一個只涉及點和直線結合關係的命題，如果將其中的點和直線及其結合關係對換得到一個新命題，稱之為原命題的對偶命題。若原命題成立，則其對偶命題也成立，這就是射影幾何里的對偶原理。在空間，點和平面是對偶元素，直線是自對偶元素，空間通過同一直線的所有平面的集合稱為面束，它與點列是空間對偶圖形，線束是自對偶圖形。
圖2 射影平面
設在射影平面上(如圖2)，兩直線l及l′，S是不在l及l′上的點，P是l上的任一點，則SP必交l′於一點P′，稱P′是點P從S投射到l′的中心投影，S稱為射心，SP稱為射線。顯然，P點也是P′在l上的中心投影，我們把二射影直線上的點經中心投影所建立的一一對應稱為點列間的透視對應，同樣可以建立兩個射影平面π和π′間的透視對應，稱為點場間的透視對應，射心則稱為透視中心;透視對應保持同素性、結合性不變。設共線4點P1、P2、P3、P的對應點分別為P′1、P′2、P′3和P′ (如圖3)，則有：
圖3 透視對應
兩點列l(x)到l′(x′)的點之間的一個一一對應，使l上任意4點的交比與l′上對應4點的交比相等，則此一一對應稱為點列l(x)到l′(x′)的射影對應;當兩個點列的底重合時，稱為點列的射影變換或一維射影變換。
兩點場π(x)及π′(x′)的點間的一個一一對應，滿足以下條件：(1)π(x)上共線3點仍變為共線3點。(2)共線4點的交比不變。則此一一對應稱為點場π(x)到點場π′(x′)的射影對應，當兩點場的底重合時，稱為點場的射影變換或二維射影變換。
由此可得點列的射影變換，就是把點列l(x)上的任意一點經過有限次的透視對應，最後仍變到點列l(x)上的點的一個變換;點場的射影變換，就是把點場π(x)上的點經過有限次的透視對應最後仍變到π(x)上的點的一個變換。根據對偶原則，還有線束的射影變換，它也是一維射影變換;線場的射影變換，它是二維射影變換等等。
射影變換的乘積是射影變換，射影變換之逆是射影變換，所以一切射影變換的集合構成一個群，稱為射影變換群，簡稱為射影群。
圖形在射影變換下不變的性質和量稱為射影性質和射影不變數;研究圖形的射影性質的幾何分支就是射影幾何學。例如結合性、分離性是基本射影性質，交比是基本射影不變數。
在射影平面上，二次曲線也可以用射影觀點來定義，一個二次曲線經射影變換後仍變為二次曲線，且在射影幾何里，橢圓、雙曲線、拋物線屬於同一等價類。
交比
亦稱複比。射影幾何的基本不變數。若四點P1，P2，P3，P4共線，則兩個單比(P1P2P3)與(P1P2P4)的比稱為P1，P2，P3，P4的交比，記為(P1P2，P3P4)。其中P1，P2稱為基點偶，P3，P4稱為分點偶。由於交比是兩個簡單比的比，故又稱它為複比。利用四個點的交比可以定義直線束中四條直線的交比以及平面束中四個平面的交比。
共線四點P1，P2，P3，P4的交比(P1P2，P3P4)有下列基本性質：
1.基點偶與分點偶交換，交比的值不變，即
2.基點偶的兩個字母交換或分點偶的兩個字母交換，交比的值變為原來交比值的倒數，即：
3.同時交換每個點偶里的字母，交比的值不變，即：
4.交換中間的兩個字母或交換兩端的兩個字母，交比的值等於1減去原來的交比值，即：
這些性質易從交比的定義或交比的代數表示推出.由這些性質知道，儘管共線四點可構成24個交比，但不同的交比值至多只有6個。若交比(P1P2，P3P4)=λ，則這六個值分別是：
