基本介紹
相關研究

基本介紹
透視對應










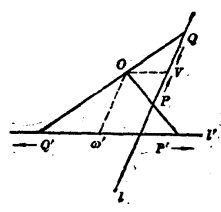
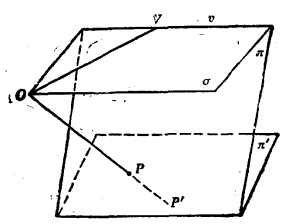
射影性質舉例





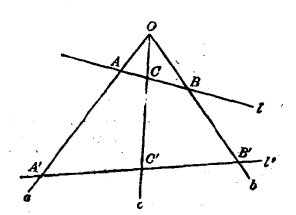



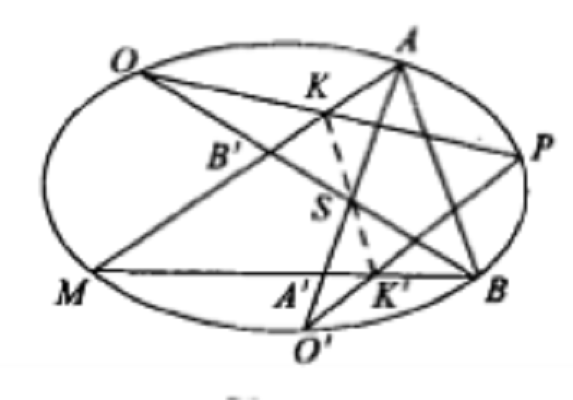






















射影性質是射影變換的一種特徵,指圖形經過任何射影對應(變換)都不變的性質,例如,非調和比、二次曲線極點與極線的關係、一條代數曲線的類型或階、同素性、結合性等都是射影性質,但平行性不是射影性質,如中心投影是射影對應,而中心...
射影是一個存在於數學及物理學中的概念,存在於集合論、線性代數、幾何學以及拓撲學等諸多理念中。在平面幾何中,與一個圖形相似的圖形叫做這個圖形的射影。射影是幾何學術語,射影幾何用來研究圖形的射影性質,即圖形經過射影變換不變的...
射影長定理 射影長定理(theorem of length of segment projection )是立體幾何中的重要定理之一。它是根據直角三角形的性質得出的。 射影幾何學 射影幾何學作為一門古老而又精妙的幾何學分支,起源於17世紀。在這個時期,兩位傑出的數學家...
論圖形的射影性質(Traite des proprietes pro-jectives des figures)西方近現代數學著作.法國數學家、力學家彭賽列(Poncelet, J. - V.)著,1822年出版.這是第一本完全致力於射影幾何學的著作.彭賽列充分認識到射影幾何學是具有獨特...
研究圖形的射影性質,即它們經過射影變換不變的性質。一度也叫做投影幾何學,在經典幾何學中,射影幾何處於一種特殊地位,通過它可以把其他一些幾何聯繫起來。擴大空間和射影空間 在一個歐氏(或仿射)平面上,兩條直線一般相交於一點,但...
射影不變數(projective invariant)是射影變換的一種特徵。指圖形經過任何射影對應(變換)都不變的量。射影不變數也是一種射影性質。例如,交比就是最基本的射影不變數,同時也是最重要的射影性質。射影幾何 亦稱投影幾何。幾何學的一個分支...
性質 n維射影空間是最簡單的不可定向的單連通緊流形(n為偶數時不可定向,奇數時可定向),也是最簡單的代數簇。n維射影空間可以用若干個開集覆蓋住, 每個開集恰是n維仿射空間。例子 射影直線 射影直線的定義是:在歐氏直線上添加一個...
射影性質指在射影變換下不變的性質。射影幾何也叫投影幾何,是幾何學的一種,也是數學的一個分支。它的某些內容,公元前就已經發現了,但直到19世紀才形成獨立體系。彭賽列(V.Poncelet)是射影幾何的主要奠基人,他是充分認識到射影幾何...
在概形理論中,還將射影空間建立在整數環Z上,即建立射影概形P。由此對任意概形X可以建立P,它是X和P(在Spec Z上)的纖維積。特別地,若X=Spec K(K為域),則P=Pn。由於射影空間的性質非常豐富難以全面列舉,僅舉數例如下:1....
射影長定理(theorem of length of segment projection )是立體幾何中的重要定理之一。它是根據直角三角形的性質得出的。定理內容 從平面外一點向這個平面所引的垂線段和斜線段中:1.射影相等的兩條斜線段相等,射影較長的斜線段...
然而,射影幾何作為幾何學的一個獨立分支學科卻是在19世紀初期,隨著幾何學的發展以及繪畫與建築的需要而形成和發展起來的。1822年,彭賽列(Poncelet,J.-V.)發表了射影幾何的第一部系統著作《論圖形的射影性質》一書。他通過幾何方法...
則可構成羅氏幾何;若絕對形為非退化的虛二階曲線,則可構成黎氏幾何,這兩種幾何合稱非歐幾何,這樣非歐幾何就可以從射影測度的概念導出,因為射影測度是由交比來定義的,它屬於射影性質,所以非歐幾何可以利用射影測度從射影幾何導出。
的擴大空間,即去掉了無窮遠點後全體有窮點的集合是歐氏空間(仿射空間),射影空間具有與歐氏空間(仿射空間)不同的性質,例如在射影空間中,任何一個平面都不能把射影空間分成兩部分,任何兩個平面都相交,但它們卻不能把射影空間分成四...
推論 直線上的射影變換,若使三個點不變(即有三個固定點),則必為恆等變換。附註一維射影對應式(3.1.1)的非齊次形式為 也可寫成 的雙線性方程 一維射影對應的特徵性質是一一對應保交比,也可說成是一一對應保調和比,事實上有...
這就有點像盲人摸象,只限於平面幾何觀點看這些曲線,覺得它們非常不同,但從射影幾何觀點下看,其實是一個東西的不同部分。性質 射影直線具有歐幾里得直線截然不同的性質。射影直線上的任何一點都不能把該直線分成兩部分;射影直線上任何...
射影坐標是在射影幾何學中和在研究圖形的純射影性質時,常採用的一種坐標系。它在射影幾何中的作用,就象直角坐標系在歐氏幾何中和仿射坐標系在仿射幾何學中的作用。基本概述 射影 射影是物體在某平面或某空間形成的投影。射影幾何 射影...
2.已知異面直線m,n,設m,n在平面α上的射影分別為直線m′,n′,則稱直線m′與n′所成的角是異面直線m,n在平面α上的射影角(異面直線的射影角).性質 1.定理: 已知∠AOB∈(0,π),總存在一個平面,使∠AOB在平面上的射影角...
研究的對象主要是曲線、曲面、共軛網等在射影變換群下的不變數、協變圖形及其性質。研究歷程 19世紀末,法國數學家達布在《曲面通論教程》(1887—1896) 和《正交系與曲線坐標》(1898)中系統介紹了近百年來曲線和曲面微分幾何學方面的...
Pⁿ(C)的一個子集,若它可以表示為定義在C中一組齊次多項式公共零點的集合,則稱它為射影代數簇,簡稱代數簇,也可稱它為Pⁿ(C)的代數子集。基本介紹 代數簇(algebraic variety)是代數幾何的基本研究對象。設k是一個域,域k上...
為一維射影變換,如果 有兩個相異的實不變元素,則稱之為一個雙曲型射影變換;如果 有兩個重合的實不變元素,則稱之為一個拋物型射影變換;如果 有兩個共軛的虛不變元素,則稱之為一個橢圓型射影變換。不變元素的性質 關於雙曲...
稱此空間為m維復射影空間。性質 的上同調群為 ,其餘的上同調群為0。為CW復形,且對每個q(0≤q≤n),都有一個2q胞腔。當q=1,n=1時,,有 ,設對應生成元為α。由於 為 的(2n-2)骨架,有相對上同調群 ,其餘的相對上...
射影決定性公理是決定性公理的一種最重要的弱形式。射影決定性公理(the axiom of projective de-terminacy)簡稱PD.決定性公理的一種最重要的弱形式.決定性公理認為,對任何Ac},w,對弈G(A)都是決定的,這一假定太強,以致與選擇...
在數學裡,映射是個術語,指兩個元素的集之間元素相互“對應”的關係,為名詞。映射,或者射影,在數學及相關的領域經常等同於函式。 基於此,部分映射就相當於部分函式,而完全映射相當於完全函式。定義 兩個非空集合A與B間存在著對應...
例如,經過剛體運動不變的性質就是度量性質,是歐氏幾何研究的對象;經過仿射變換不變的性質就是仿射性質,是仿射幾何研究的內容;經過射影變換不變的性質就是射影性質,是射影幾何的研究內容。距離、角度、面積、平行性、單比、交比等在...
關於相似群的圖形的不變性質和不變數分別稱為相似性質和相似不變數,如角度等,研究相似性質和相似不變數的幾何稱為相似幾何。關於射影群的圖形的不變性質和不變數分別稱為射影性質和射影不變數,如同素性、結合性、交比等,研究射影性質...
例如:經過運動不變的性質就是度量性質,研究度量性質的幾何叫做度量幾何(歐氏幾何);經過仿射變換不變的性質就是仿射性質,研究仿射性質的幾何叫做仿射幾何;經過射影變換不變的性質就是射影性質,研究射影性質的幾何叫做射影幾何;等等。...
對角映射(diagonal mapping)是標準內射的和。在數學裡,映射是個術語,指兩個元素的集之間元素相互“對應”的關係,為名詞。映射,或者射影,在數學及相關的領域經常等同於函式。 基於此,部分映射就相當於部分函式,而完全映射相當於完全...
從十七世紀開始,幾何學家在研究投影和截面取景時的方法和結果,大大地豐富了歐氏幾何的內容,並逐漸認識到這是幾何學一個新的分支,稱之為射影幾何學。射影幾何是研究圖形的射影性質,即它們經過射影變換後,依然保持不變的圖形性質的...
他在1822年寫的《論圖形的射影性質》(在巴黎出版)和在1824年提交巴黎科學院的《衍合配極的一般理論》中,給出了極點和極線相互變換的一般表述,並以此建立了許多定理。不過,在這一時期,他利用配極來建立的對偶原理,是需要一個圓錐...
