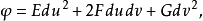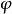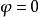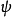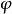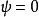射影微分幾何學

射影微分幾何（projective differential geometry）是微分幾何的一個分支，研究幾何圖形關於空間射影變換不變的微分幾何性質．例如曲面的共軛網、漸近方向都是研究的對象。兩個參數曲線族的疊合理論是射影微分幾何的主要內容。在這一理論中研究焦曲面和可展曲面、焦點等。

基本介紹

• 中文名：射影微分幾何學
• 外文名：projective differential geometry
• 所屬學科：數學
• 所屬領域：微分幾何的一個分支
• 屬性：射影變換群
• 相關人物：克萊因、富比尼、嘉當、蘇步青等

簡介

射影微分幾何學(projective differential geometry)從屬於射影變換群。其思想來源於C.F.克萊因1872年的著名演說“埃朗根綱領”，在那裡將幾何學歸結為可逆變換群的幾何不變數理論加以分類。研究的對象主要是曲線、曲面、共軛網等在射影變換群下的不變數、協變圖形及其性質。

研究歷程

19世紀末，法國數學家達布在《曲面通論教程》(1887—1896) 和《正交系與曲線坐標》(1898)中系統介紹了近百年來曲線和曲面微分幾何學方面的成就，其中蘊含了射影微分幾何學的萌芽。同時代的數學家阿爾方也對射影微分幾何做過系統研究。1906年德國—美國數學家維爾欽斯基發表論著《曲線和直紋曲面的射影微分幾何》，將曲線的射影微分幾何理論推廣到曲面上，成為現代射影微分幾何的創始人之一。其後義大利數學家富比尼用一種射影不變的方法獲得“富比尼規範坐標”，詳盡闡述了系統研究曲線和曲面的過程。他與捷克數學家切赫合著的《射影微分幾何》(2卷，1926—1927)與《曲面射影微分幾何引論》(1931)已成為該學科的經典著作。

1937年法國數學家É.嘉當出版《射影聯絡空間理論教程》，創立新的活動標架法，重新建立起射影曲面論，振興了微分幾何學。他引入一般纖維叢理論，構造了仿射、射影及保形的廣義联絡空間，他的外形法為現代高維射影空間共軛網理論提供了依據。此外，義大利數學家邦皮亞尼和中國數學家蘇步青都對射影微分幾何做過系統的研究工作。蘇步青從20世紀30年代末開創並發展起結構式射影微分幾何，用幾何作圖法建立協變的構圖和不變數，特別是用平面曲線在某種奇異點的不變數以表達其他幾何不變數，這是一項具有代表性的顯著成果。他的有關著作有《射影曲線概論》(1954)、《射影曲面概論》(1964)、《射影共軛網概論》(1978)等。

三種研究方法

射影微分幾何是從屬於射影變換群的微分幾何，在達布的著名的曲面論中已含有它的萌芽，它主要是在20世紀初期按照克萊因的思想展開的，到20世紀40年代趨於完善。主要研究對象是曲線、曲面和共軛網等在射影變換群下的不變數、協變圖形及其性質。

射影微分幾何的研究方法大致有下列三種：

第一種是以富比尼(G.Fubini)為首的義大利學派的方法。以曲面論為例，設是三維射影空間中齊次坐標，是曲面S的參數表示，用一種射影不變的方法確定的比例因子，得到富比尼規範坐標，構造二次和三次形式：

式中和普通曲面論中第二基本形式只相差一個因子，於是定義了曲面的兩族漸近曲線，和滿足配極關係，定義曲面的三族達布曲線，這兩個基本形式的係數滿足一系列關係式，即曲面的基本方程，同普通曲面論一樣，可導出射影曲面論的基本定理。

第二種是嘉當(E.Cartan)的活動標架法。嘉當用活動標架法重建射影曲面論，問題歸結為普法夫方程組，可積條件即嘉當結構方程，從而導出許多結果，近年來，用嘉當方法發展起來高維射影空間共軛網理論。

第三種是以蘇步青為首的中國學者開創和發展的結構式射影微分幾何方法，主要是用幾何作圖法來建立射影協變的構圖和不變數。例如用平面曲線在其某種奇點的不變數來表達其他的幾何不變數。