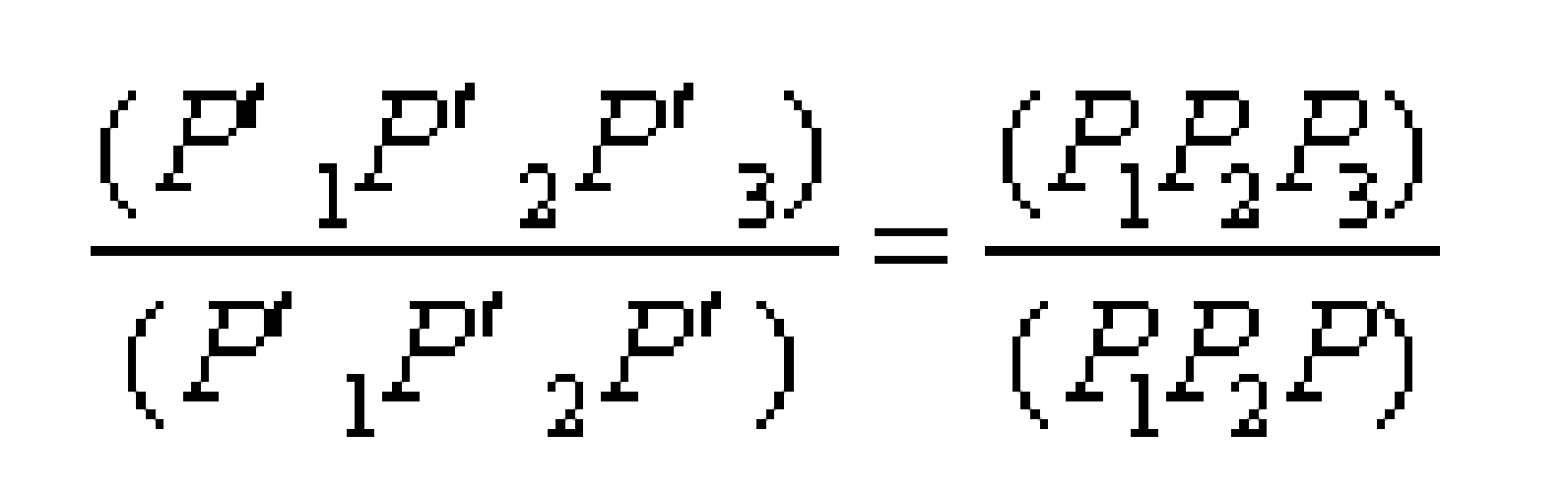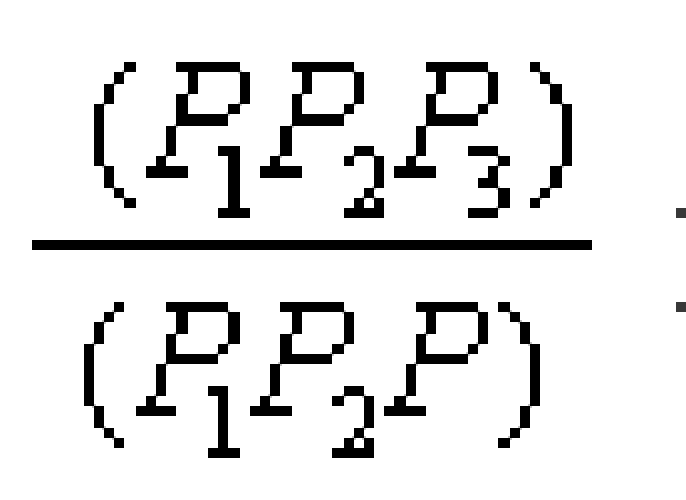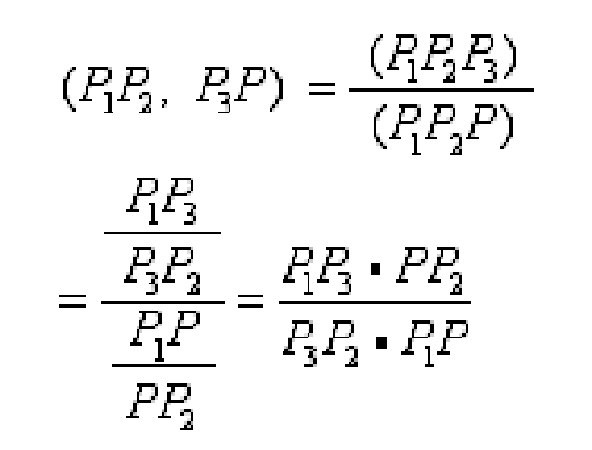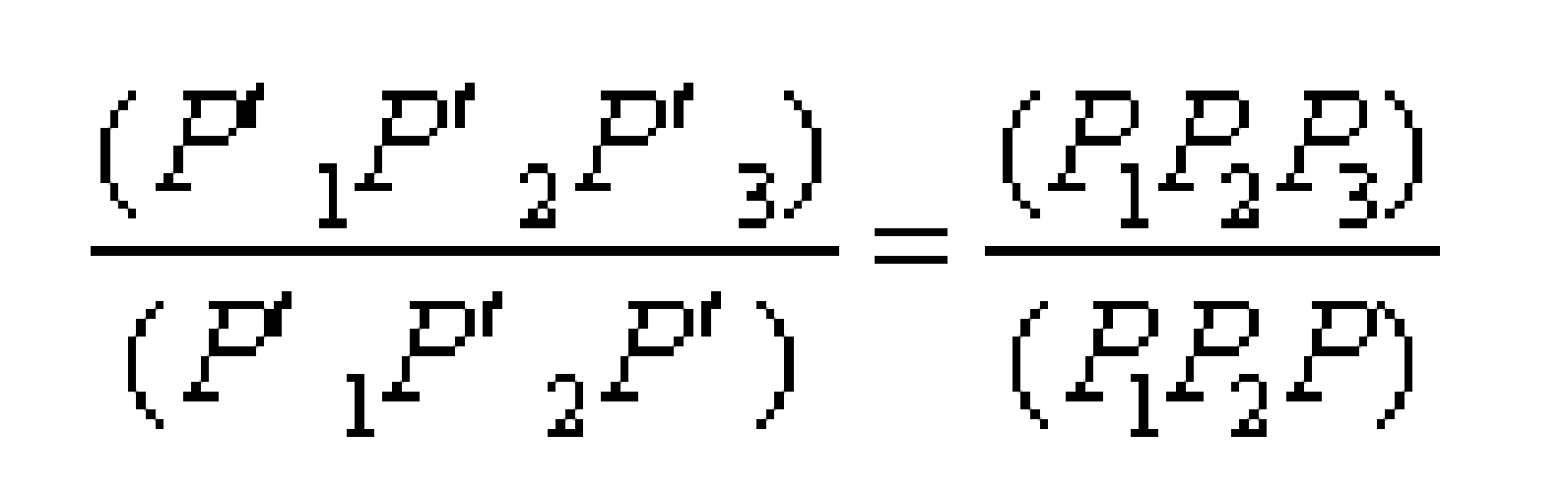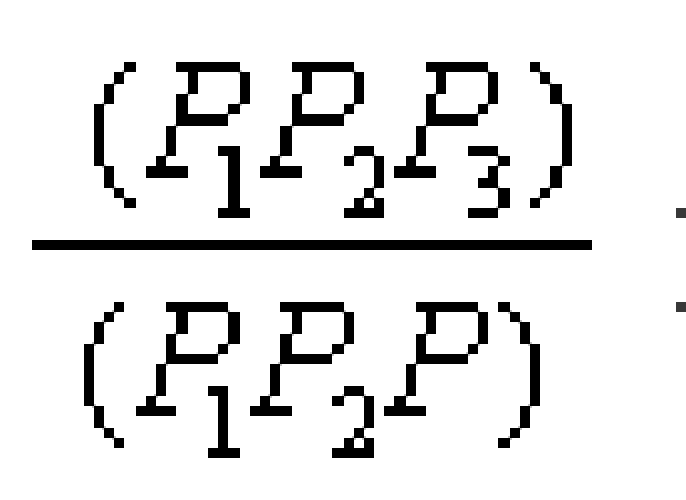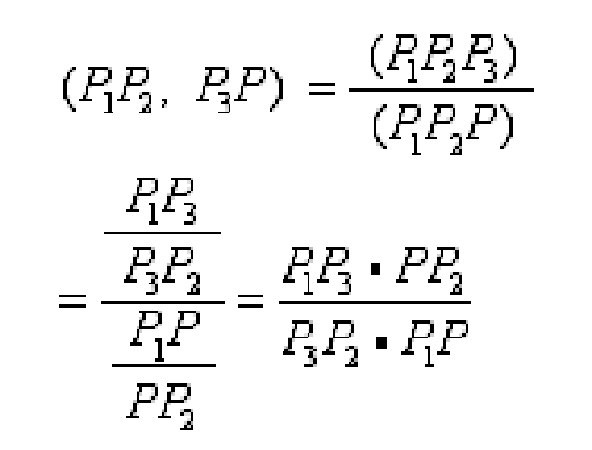基本介紹
- 中文名：對射變換
- 外文名：correlation
- 領域：數學
- 性質：射影變換
- 意義：指平面上點與直線的一一對應
- 空間：射影空間
概念,射影變換,射影空間,
概念
對射變換(correlation)是一種基本射影變換。指平面上點與直線或直線與點間的一一對應。平面到自身的對射變換由下列關係式確定：
其中(xi)是平面上點的射影坐標，(u′i)是與(xi)對應的直線的線坐標。
射影變換
在歐氏平面上，對於“一組有定方位的一切直線”添加一個點稱為該方位的無窮遠點，此點在該組中的每一直線上，而不在這組以外的直線上;為了區分，以前所見的點稱為有窮點;由於不同方位的直線有不同的無窮遠點，這樣，平面上一切無窮遠點的集合組成一條直線稱為無窮遠直線，以前所見的直線稱為有窮直線； 一組平行平面相交於一條無窮遠直線。空間內一切無窮遠點的集合組成一個平面稱為無窮遠平面，以前所見的平面稱為有窮平面。無窮遠點、無窮遠直線、無窮遠平面統稱之為無窮遠元素。
在歐氏平面上添加了一個無窮遠點後，得到一條新的直線，我們將它稱為仿射直線;如果把仿射直線上的有窮點和無窮遠點等同看待而不加區分，則這條直線就稱為射影直線(如圖1)。歐氏直線a上添加一個無窮遠點，記作P∞，就得到一條仿射直線;反過來，如果將射影直線上某一定點認為是無窮遠點，而將其餘點定為有窮點，即得到一條仿射直線，仿射直線上有窮點和無窮遠點不加區分就是一條射影直線，故得射影直線可看作是封閉的，歐氏平面上的圓，常可以作為射影直線的模型。
圖1 射影直線
仿此，在歐氏平面上，添加一條無窮遠直線，記作l∞，即得到一個仿射平面，在仿射平面上有窮、無窮不加區分就是射影平面(二維射影空間)： 反之，如將射影平面內去掉一條直線就轉到歐氏平面了。在歐氏三維空間，添加一個無窮遠平面，記作π∞，即得到仿射空間，仿射空間內有窮、無窮不加區分就是射影空間。在射影空間裡，任何兩條直線、一直線與一個平面至少有一個交點;任何兩個平面必相交於一條直線，任意兩點決定一條直線; 任意不共線的3點必決定一個平面，任意不共線的3個平面必恰有一個交點。由上面的結論可以看出，結合關係是射影平面和射影空間的基本關係。點在直線上與直線通過點有完全的對稱性，也就是使得點和直線在邏輯上取得平等的地位，它們稱為平面上的對偶元素，我們把平面上一個以點和直線構成的圖形，把其中的點和直線互換就得到一個新的圖形稱為已知圖形的對偶圖形，如平面內 “在一直線上一切點的集合” 稱為以該直線為底的點列和平面內 “通過同一點的一切直線的集合”稱為以定點為中心的線束，二者互為對偶圖形。在一個平面上，一切點的集合稱為點場和一切直線的集合稱為線場，點場和線場也是平面對偶圖形; 平面上，一個只涉及點和直線結合關係的命題，如果將其中的點和直線及其結合關係對換得到一個新命題，稱之為原命題的對偶命題。若原命題成立，則其對偶命題也成立，這就是射影幾何里的對偶原理。在空間，點和平面是對偶元素，直線是自對偶元素，空間通過同一直線的所有平面的集合稱為面束，它與點列是空間對偶圖形，線束是自對偶圖形。
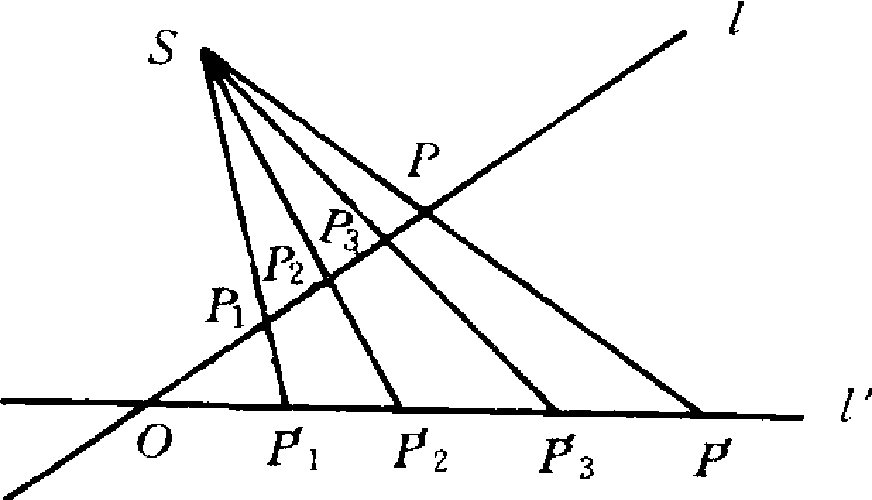
圖2 射影平面
設在射影平面上(如圖2)，兩直線l及l′，S是不在l及l′上的點，P是l上的任一點，則SP必交l′於一點P′，稱P′是點P從S投射到l′的中心投影，S稱為射心，SP稱為射線。顯然，P點也是P′在l上的中心投影，我們把二射影直線上的點經中心投影所建立的一一對應稱為點列間的透視對應，同樣可以建立兩個射影平面π和π′間的透視對應，稱為點場間的透視對應，射心則稱為透視中心;透視對應保持同素性、結合性不變。設共線4點P1、P2、P3、P的對應點分別為P′1、P′2、P′3和P′ (如圖3)，則有：
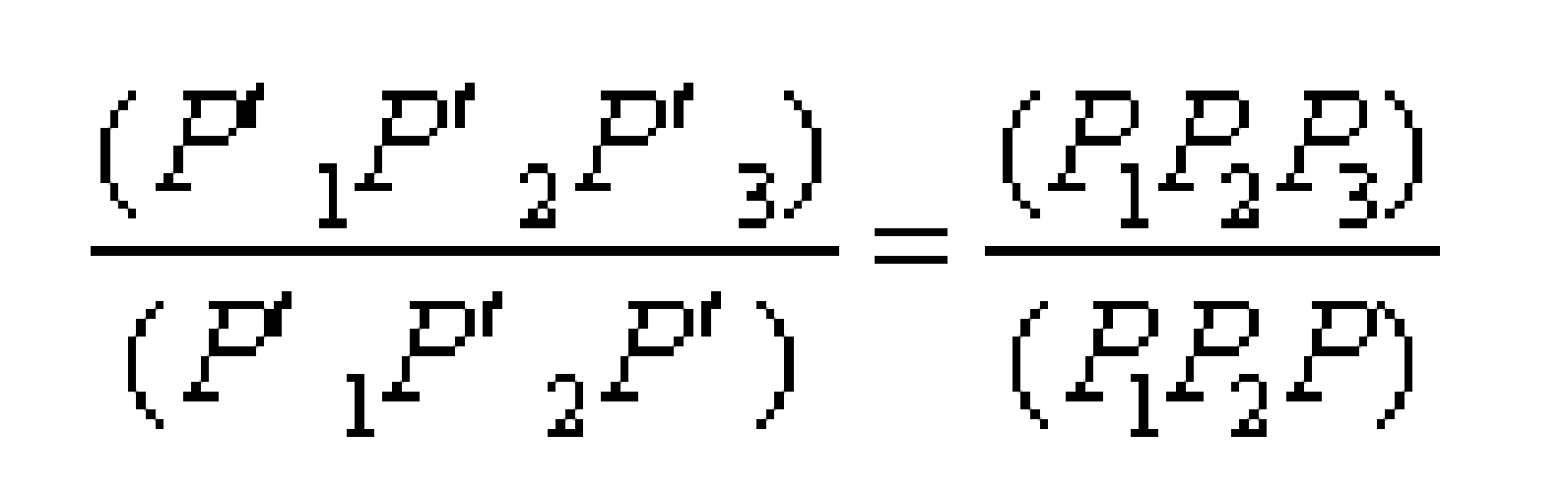
圖3 透視對應
稱：
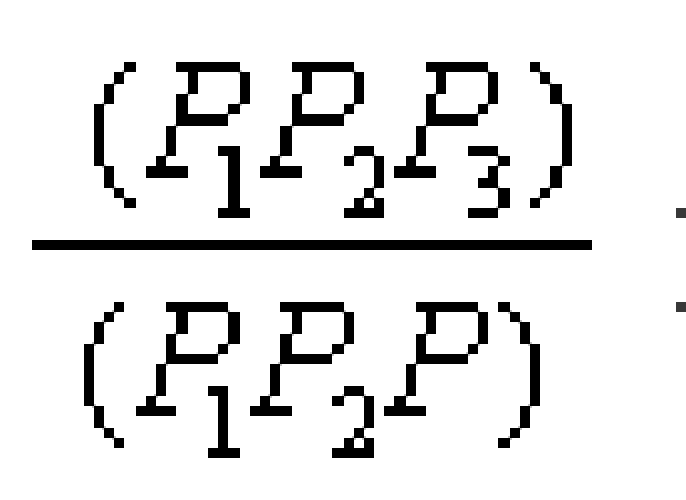
圖4 透視對應
為共線4點P1、P2、P3、P的交比，其中P1、P2為基點偶，P3、P為分點偶，P1、P2、P3、P4點的交比記作(P1P2，P3P)，即：
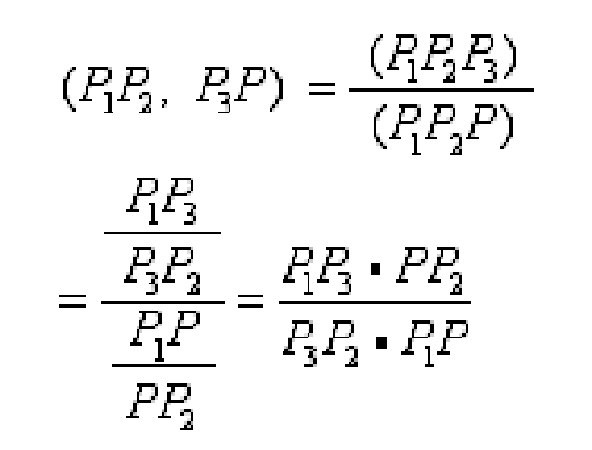
圖5 透視對應
(其中線段均為有向線段)。容易看出，當P3、P兩點均屬於或均不屬於線段P1P2時，則交比為正，這時我們說點偶P1、P2不分離點偶P3、P;在另一種情形，則說點偶P1、P2分離點偶P3、P，此時交比為負。故說透視對應保持分離性不變，交比是透視對應下基本不變數。
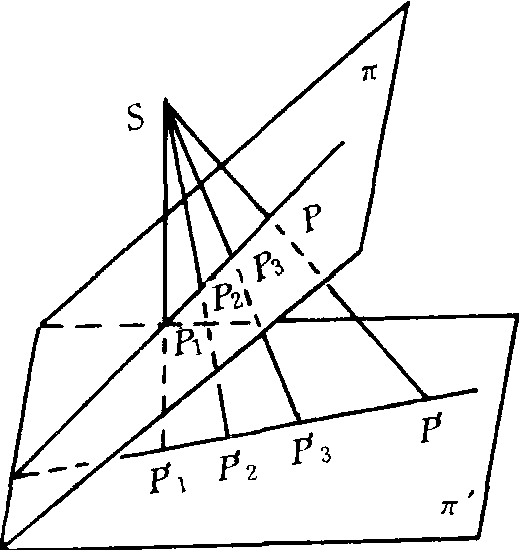
圖6 透視對應
兩點列l(x)到l′(x′)的點之間的一個一一對應，使l上任意4點的交比與l′上對應4點的交比相等，則此一一對應稱為點列l(x)到l′(x′)的射影對應；當兩個點列的底重合時，稱為點列的射影變換或一維射影變換。
兩點場π(x)及π′(x′)的點間的一個一一對應，滿足以下條件：(1)π(x)上共線3點仍變為共線3點。(2)共線4點的交比不變。則此一一對應稱為點場π(x)到點場π′(x′)的射影對應，當兩點場的底重合時，稱為點場的射影變換或二維射影變換。
由此可得點列的射影變換，就是把點列l(x)上的任意一點經過有限次的透視對應，最後仍變到點列l(x)上的點的一個變換;點場的射影變換，就是把點場π(x)上的點經過有限次的透視對應最後仍變到π(x)上的點的一個變換。根據對偶原則，還有線束的射影變換，它也是一維射影變換；線場的射影變換，它是二維射影變換等等。
射影變換的乘積是射影變換，射影變換之逆是射影變換，所以一切射影變換的集合構成一個群，稱為射影變換群，簡稱為射影群。
射影空間
整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形)，為方便起見引入無窮遠點的概念，即規定平面上每條直線上有一個無窮遠點，兩條直線平行就是相交於無窮遠點，所有無窮遠點組成一條無窮遠直線。這種構造方法還可以推廣到高維空間，建立n維(實)射影空間PR。在n維射影空間中常採用齊次坐標(X0∶X1∶…∶Xn)，其中X0，X1，…，Xn不全為0;若a≠0，則(aX0∶aX1∶…∶aXn)與(X0∶X1∶…∶Xn)表示同一個點。因此n維(實)射影空間同構於(R-{0})/R.進一步的研究表明PR是緊緻解析流形。若令Ui(0≤i≤n)為PR中坐標Xi≠0的點全體，則UiR，且U0，U1，…，Un組成PR的一個開覆蓋。上述構造方法可以推廣到任意體K上，建立K上的n維射影空間PK.在概形理論中，還將射影空間建立在整數環Z上，即建立射影概形PZ。由此對任意概形X可以建立PX，它是X和PZ(在Spec Z上)的纖維積。特別地，若X=Spec K(K為域)，則PX=PK。
由於射影空間的性質非常豐富難以全面列舉，僅舉數例如下：
1.PR同胚於圓，PC可看做添上無窮遠點的複平面，同胚於球面。
2.PR是單側曲面，可以同胚地嵌入四維空間R，但不能同胚地嵌入三維空間R，PC是代數極小曲面。
3.PC是克勒流形，它的閉解析子空間都是代數的。
4.對任意域k，Pk是齊性空間，其切叢由整體向量場生成，其自同構群為射影群PSL(n+1，k)，其皮卡群Pic(Pk)Z。
