交點式是拋物線的一種數學表達形式，即用拋物線與x軸的兩個交點來表示拋物線的函式形式。
基本介紹
- 中文名：交點式
- 外文名：Intersection formula
- 性質：數學概念
- 考點：四個考點
主要概述,交點式分類,二次函式性質,四大考點,考點一,考點二,考點三,考點四,
主要概述
二次函式與x軸交點圖像交點式：y=a(x-x1)(x-x2)+y 僅限於A(x1,y)、B(x2,y) [x1與x2所對應的y相等]
也有國中老師給的交點式為y=a(x+x1)(x+x2)，式中的x1,x2為x1,x2的相反數。（帶入數據後，同上）。
在解決與二次函式的圖象和x軸交點坐標有關的問題時，使用交點式較為方便。y=a(x-x1)(x-x2) 找到函式圖象與X軸的兩個交點，分別記為x1和x2,代入公式，再有一個經過拋物線的點的坐標，即可求出a的值。 將a、X1、X2帶入y=a(x-x1)(x-x2)，即可得到一個解析式，這是y=ax2+bx+c因式分解得到的，將括弧打開，即為一般式。X1,X2是關於ax^2+bx+c=0的兩個根。
交點式的推導1
則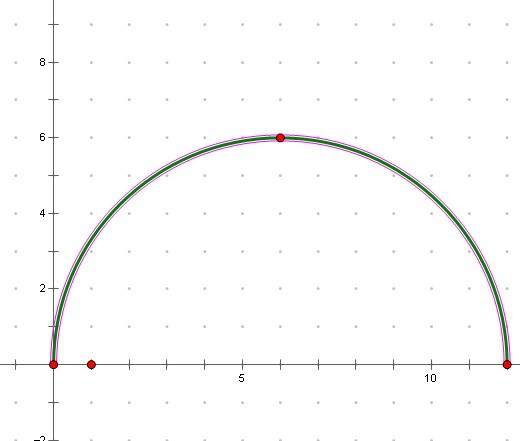
因為需要求與x軸的交點，所以
，而a不等於0
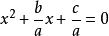
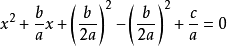
一般這種題用十字相乘因式分解即可
交點式的推導2
設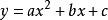
函式與x軸有兩交點,即
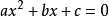有兩個根分別為
,
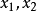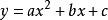
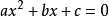
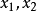
根據韋達定理
十字交叉相乘：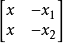
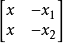
得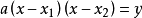
。
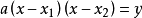
交點式分類
其他形式解決二次函式，還有一般式和頂點式
一般式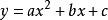：（a≠0）
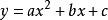
頂點式：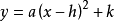
（a≠0）頂點坐標（h，k）
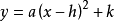
交點式：
（a≠0）[僅限於與x軸有交點A（x1，0）和 B（x2，0）的拋物線]
二次函式性質
（1）拋物線 的頂點是坐標原點，對稱軸是y軸.
（2）函式y=ax2+bx+c的圖像與x的符號關係. ①當x<0 時,拋物線開口向上 頂點為其最低點； ②當x>0時 拋物線開口向下 頂點為其最高點.
（3）頂點是坐標原點，對稱軸是y軸的拋物線的解析式形式為y=ax2+bx+c .
3.二次函式 的圖像是對稱軸平行於（包括重合）y 軸的拋物線.
4.二次函式 用配方法可化成：y=ax2+bx+c 的形式，其中a≠0.
5.二次函式由特殊到一般，可分為以下幾種形式：① ；② ；③ ；④ ；⑤ .
6.拋物線的三要素：開口方向、對稱軸、頂點.
①x的符號決定拋物線的開口方向：當x<0 時，開口向上；當x>0時，開口向下；y相等，拋物線的開口大小、形狀相同.
②平行於y 軸（或重合）的直線記作直線x=0 .特別地，y軸記作直線 .
8.求拋物線的頂點、對稱軸的方法
（1）公式法： ，∴頂點是 ，對稱軸是直線 .
（2）配方法：運用配方的方法，將拋物線的解析式化為 的形式，得到頂點為( , )，對稱軸是直線 .
9.拋物線 中， 的作用
（1） 決定開口方向及開口大小，這與 中的 完全一樣.
（2） 和 共同決定拋物線對稱軸的位置.由於拋物線 的對稱軸是直線 ，故：
① 時，對稱軸為 軸；② （即 、 同號）時，對稱軸在 軸左側；
③ （即 、 異號）時，對稱軸在 軸右側.
（3） 的大小決定拋物線 與 軸交點的位置. 當 時， ，∴拋物線 與 軸有且只有一個交點（0， ）
① ，拋物線經過原點;
② ,與 軸交於正半軸；
③ ,與 軸交於負半軸. 以上三點中，當結論和條件互換時，仍成立.如拋物線的對稱軸在 軸右側，則 .
10.幾種特殊的二次函式的圖像特徵如下：
11.用待定係數法求二次函式的解析式
（1）一般式： .已知圖像上三點或三對 、 的值，通常選擇一般式.
（3）交點式：已知圖像與 軸的交點坐標 、 ，通常選用交點式： .
12.直線與拋物線的交點
（1） 軸與拋物線 得交點為(0, ).
（2）與 軸平行的直線 與拋物線 有且只有一個交點( , ).
①有兩個交點 拋物線與 軸相交；
②有一個交點（頂點在 軸上） 拋物線與 軸相切；
③沒有交點 拋物線與 軸相離.
（4）平行於 軸的直線與拋物線的交點 同（3）一樣可能有0個交點、1個交點、2個交點.當有2個交點時，兩交點的縱坐標相等，設縱坐標為 ，則橫坐標是 的兩個實數根.
①方程組有兩組不同的解時 與 有兩個交點;
②方程組只有一組解時 與 只有一個交點；
③方程組無解時 與 沒有交點.
四大考點
考點一
平面直角坐標系（3分） 1、平面直角坐標系 在平面內畫兩條互相垂直且有公共原點的數軸，就組成了平面直角坐標系。 其中，水平的數軸叫做x軸或橫軸，取向右為正方向；鉛直的數軸叫做y軸或縱軸，取向上為正方向；兩軸的交點O（即公共的原點）叫做直角坐標系的原點；建立了直角坐標系的平面，叫做坐標平面。 為了便於描述坐標平面內點的位置，把坐標平面被x軸和y軸分割而成的四個部分，分別叫做第一象限、第二象限、第三象限、第四象限。 注意：x軸和y軸上的點，不屬於任何象限。 2、點的坐標的概念 點的坐標用（a，b）表示，其順序是橫坐標在前，縱坐標在後，中間有“，”分開，橫、縱坐標的位置不能顛倒。平面內點的坐標是有序實數對，當 時，（a，b）和（b，a）是兩個不同點的坐標。
考點二
不同位置的點的坐標的特徵（3分） 1、各象限內點的坐標的特徵 點P(x,y)在第一象限 點P(x,y)在第二象限 點P(x,y)在第三象限 點P(x,y)在第四象限 2、坐標軸上的點的特徵 點P(x,y)在x軸上 ，x為任意實數 點P(x,y)在y軸上 ，y為任意實數 點P(x,y)既在x軸上，又在y軸上 x，y同時為零，即點P坐標為（0，0） 3、兩條坐標軸夾角平分線上點的坐標的特徵 點P(x,y)在第一、三象限夾角平分線上 x與y相等 點P(x,y)在第二、四象限夾角平分線上 x與y互為相反數 4、和坐標軸平行的直線上點的坐標的特徵 位於平行於x軸的直線上的各點的縱坐標相同。 位於平行於y軸的直線上的各點的橫坐標相同。 5、關於x軸、y軸或遠點對稱的點的坐標的特徵 點P與點p’關於x軸對稱 橫坐標相等，縱坐標互為相反數 點P與點p’關於y軸對稱 縱坐標相等，橫坐標互為相反數 點P與點p’關於原點對稱 橫、縱坐標均互為相反數 6、點到坐標軸及原點的距離 點P(x,y)到坐標軸及原點的距離： （1）點P(x,y)到x軸的距離等於 （2）點P(x,y)到y軸的距離等於 （3）點P(x,y)到原點的距離等於
考點三
函式及其相關概念（3~8分） 1、變數與常量 在某一變化過程中，可以取不同數值的量叫做變數，數值保持不變的量叫做常量。 一般地，在某一變化過程中有兩個變數x與y，如果對於x的每一個值，y都有唯一確定的值與它對應，那么就說x是自變數，y是x的函式。 2、函式解析式 用來表示函式關係的數學式子叫做函式解析式或函式關係式。 使函式有意義的自變數的取值的全體，叫做自變數的取值範圍。 3、函式的三種表示法及其優缺點 （1）解析法 兩個變數間的函式關係，有時可以用一個含有這兩個變數及數字運算符號的等式表示，這種表示法叫做解析法。 （2）列表法 把自變數x的一系列值和函式y的對應值列成一個表來表示函式關係，這種表示法叫做列表法。 （3）圖像法 用圖像表示函式關係的方法叫做圖像法。 4、由函式解析式畫其圖像的一般步驟 （1）列表：列表給出自變數與函式的一些對應值 （2）描點：以表中每對對應值為坐標，在坐標平面內描出相應的點 （3）連線：按照自變數由小到大的順序，把所描各點用平滑的曲線連線起來。
