二次函式交點式

交點式：y=a(X-x1)(X-x2) [僅限於與x軸有交點A（x1，0）和 B（x2，0）的拋物線]

基本介紹

• 中文名：二次函式交點式
• 形式：y=a(X-x1)(X-x2)
• 類別：數學算法
• 套用領域：中學數學
• 圖線表示：拋物線
• 交點默認：與X軸相交的點

公式含義

交點式：y=a(X-x1)(X-x2)[僅限於與x軸有交點A（x1，0）和 B（x2，0）的拋物線]

在解決與二次函式的圖象和x軸交點坐標有關的問題時，使用交點式較為方便。y=a(x-x1)(x-x2) 找到函式圖象與X軸的兩個交點，分別記為x1和x2,代入公式，再有一個經過拋物線的點的坐標，即可求出a的值。 將a、X1、X2代入y=a(x-x1)(x-x2)，即可得到一個解析式，這是y=ax²;+bx+c因式分解得到的，將括弧打開，即為一般式。X1,X2是關於ax²+bx+c=0的兩個根。

交點式的推導

設y=ax²+bx+c此函式與x軸有兩交點,, 即ax²+bx+c=0有兩根 分別為 x1,x2,

a(x²+bx/a+c/a)=0 根據韋達定理 a[x²-(x1+x2)x+x1*x2]=0

十字交叉相乘：

1x -x1

1x -x2

a(x-x1)(x-x2) 就是這樣推出的。

解決二次函式，還有一般式和頂點式

一般式：y=ax²+bx+c

頂點式：y=a(x-h)²+k

交點式：y=a(x-x1)(x-x2) [僅限於與x軸有交點A（x1，0）和 B（x2，0）的拋物線]

一般的，如果a，b，c是常數(a≠0)，那么y叫做x的二次函式。

2.二次函式 的性質

（1）拋物線的頂點是坐標原點，對稱軸是y 軸.

（2）函式 的圖像與 的符號關係.

①當 時拋物線開口向上 頂點為其最低點；

②當 時拋物線開口向下 頂點為其最高點.

（3）頂點是坐標原點，對稱軸是 軸的拋物線的解析式形式為 .

3.二次函式 的圖像是對稱軸平行於（包括重合）y 軸的拋物線.

4.二次函式 用配方法可化成： 的形式，其中 .

5.二次函式由特殊到一般，可分為以下幾種形式：① ；② ；③ ；④ ；⑤ .

6.拋物線的三要素：開口方向、對稱軸、頂點.

①a 的符號決定拋物線的開口方向：當a>0 時，開口向上；當a<0 時，開口向下；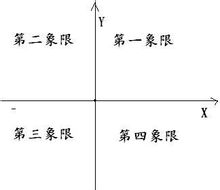

相等，拋物線的開口大小、形狀相同.

②平行於 y軸（或重合）的直線記作對稱軸 .特別地， y軸記作直線 .

7.頂點決定拋物線的位置.幾個不同的二次函式，如果二次項係數相同，那么拋物線的開口方向、開口大小完全相同，只是頂點的位置不同.

8.求拋物線的頂點、對稱軸的方法（1）公式法： ，∴頂點是 ，對稱軸是直線 .

（2）配方法：運用配方的方法，將拋物線的解析式化為 的形式，得到頂點為( , )，對稱軸是直線 .

（3）運用拋物線的對稱性：由於拋物線是以對稱軸為軸的軸對稱圖形，所以對稱軸的連線的垂直平分線是拋物線的對稱軸，對稱軸與拋物線的交點是頂點.

用配方法求得的頂點，再用公式法或對稱性進行驗證，才能做到萬無一失.

9.拋物線 中a 的作用

（1）a決定拋物線的開口，a>0, 開口向上；a<0,開口向下。

（2） |a|的大小決定拋物線的開口的大小，|a|越大，開口越小，反之|a|越小，開口越大。

（3） |a|的大小決定拋物線 與 x軸交點的位置.

當 △=0時，即b²-4ac=0時 ，拋物線 與x 軸有且只有一個交點（- ，0 ）：

10、拋物線中c的作用

①當c=0時 ，拋物線經過原點;

② 當c>0時,拋物線與y 軸交於正半軸；

③ 當c<0時,拋物線與 y軸交於負半軸.

以上三點中，當結論和條件互換時，仍成立.如拋物線的對稱軸在 軸右側，則 .

11.幾種特殊的二次函式的圖像特徵如下：

特殊的二次函式圖像

12.用待定係數法求二次函式的解析式

（1）一般式：【y=ax²+bx+c】.已知圖像上三點或三對x,y的值,通常選擇一般式.

（2）頂點式：【y=a(x－h)²+k】.已知圖像的頂點或對稱軸,通常選擇頂點式.
（3）交點式：已知圖像與x軸的交點坐標x1,x2,通常選用交點式：【y=a(x－x1)(x－x2).】

1.直線與拋物線的交點

（1） 軸與拋物線 得交點為(0, ).

（2）與 y軸平行的直線 與拋物線有且只有一個交點( , ).

（3）拋物線與 x軸的交點

二次函式 的圖像與 x軸的兩個交點的橫坐標 ，是對應一元二次方程的兩個實數根.拋物線與x 軸的交點情況可以由對應的一元二次方程的根的判別式判定：

①有兩個交點拋物線與x 軸相交；

②有一個交點（頂點在 x軸上）拋物線與 x軸相切；

③沒有交點拋物線與 x軸相離.

（4）平行於 x軸的直線與拋物線的交點

同（3）一樣可能有0個交點、1個交點、2個交點.當有2個交點時，兩交點的縱坐標相等，設縱坐標為 ，則橫坐標是 的兩個實數根.

（5）一次函式的圖像 與二次函式 的圖像 的交點，由方程組的解的數目來確定：①方程組有兩組不同的解時 與 有兩個交點; ②方程組只有一組解時 與 只有一個交點；③方程組無解時 與 沒有交點.

（6）拋物線與 軸兩交點之間的距離：若拋物線 與 軸兩交點為 ，由於 、 是方程 的兩個根，故

一次函式與反比例函式

考點一、平面直角坐標系（3分）

1、平面直角坐標系

在平面內畫兩條互相垂直且有公共原點的數軸，就組成了平面直角坐標系。

其中，水平的數軸叫做x軸或橫軸，取向右為正方向；鉛直的數軸叫做y軸或縱軸，取向上為正方向；兩軸的交點O（即公共的原點）叫做直角坐標系的原點；建立了直角坐標系的平面，叫做坐標平面。

為了便於描述坐標平面內點的位置，把坐標平面被x軸和y軸分割而成的四個部分，分別叫做第一象限、第二象限、第三象限、第四象限。

注意：x軸和y軸上的點，不屬於任何象限。

2、點的坐標的概念

點的坐標用（a，b）表示，其順序是橫坐標在前，縱坐標在後，中間有“，”分開，橫、縱坐標的位置不能顛倒。平面內點的坐標是有序實數對，當 時，（a，b）和（b，a）是兩個不同點的坐標。

考點二、不同位置的點的坐標的特徵（3分）

1、各象限內點的坐標的特徵

點P(x,y)在第一象限：X>0，Y>0

點P(x,y)在第二象限：X0

點P(x,y)在第三象限：X<0，Y<0

點P(x,y)在第四象限：X>0，Y<0

2、坐標軸上的點的特徵

點P(x,y)在x軸上 ，x為任意實數，y=0

點P(x,y)在y軸上 ，y為任意實數，x=0

點P(x,y)既在x軸上，又在y軸上 x，y同時為零，即點P坐標為（0，0）

3、兩條坐標軸夾角平分線上點的坐標的特徵

點P(x,y)在第一、三象限夾角平分線上 x與y相等

點P(x,y)在第二、四象限夾角平分線上 x與y互為相反數

4、和坐標軸平行的直線上點的坐標的特徵

位於平行於x軸的直線上的各點的縱坐標相同。

位於平行於y軸的直線上的各點的橫坐標相同。

5、關於x軸、y軸或原點對稱的點的坐標的特徵

點P與點p’關於x軸對稱 ：橫坐標相等，縱坐標互為相反數

點P與點p’關於y軸對稱 ：縱坐標相等，橫坐標互為相反數

點P與點p’關於原點對稱 ：橫、縱坐標均互為相反數

6、點到坐標軸及原點的距離

點P(x,y)到坐標軸及原點的距離：

（1）點P(x,y)到x軸的距離等於：y的絕對值

（2）點P(x,y)到y軸的距離等於：x的絕對值

（3）點P(x,y)到原點的距離等於：（x²+y²）的算數平方根

考點三、函式及其相關概念（3~8分）

1、變數與常量

在某一變化過程中，可以取不同數值的量叫做變數，數值保持不變的量叫做常量。

一般地，在某一變化過程中有兩個變數x與y，如果對於x的每一個值，y都有唯一確定的值與它對應，那么就說x是自變數，y是x的函式。

2、函式解析式

用來表示函式關係的數學式子叫做函式解析式或函式關係式。

使函式有意義的自變數的取值的全體，叫做自變數的取值範圍。

3、函式的三種表示法及其優缺點

（1）解析法

兩個變數間的函式關係，有時可以用一個含有這兩個變數及數字運算符號的等式表示，這種表示法叫做解析法。

（2）列表法

把自變數x的一系列值和函式y的對應值列成一個表來表示函式關係，這種表示法叫做列表法。

（3）圖像法

用圖像表示函式關係的方法叫做圖像法。

4、由函式解析式畫其圖像的一般步驟

（1）列表：列表給出自變數與函式的一些對應值

（2）描點：以表中每對對應值為坐標，在坐標平面內描出相應的點

（3）連線：按照自變數由小到大的順序，把所描各點用平滑的曲線連線起來。

考點四、正比例函式和一次函式（3~10分）

1、正比例函式和一次函式的概念

一般地，如果 （k，b是常數，k 0），那么y叫做x的一次函式。

特別地，當一次函式中的b為0時， （k為常數，k 0）。這時，y叫做x的正比例函式。

2、一次函式的圖像

所有一次函式的圖像都是一條直線

3、一次函式、正比例函式圖像的主要特徵：一次函式 的圖像是經過點（0，b）的直線；正比例函式 的圖像是經過原點（0，0）的直線。