基本介紹
- 中文名:配方法
- 外文名:method of completing the square
- 拼音:pèi fāng fǎ
- 相關領域:數學,計算
- 用途:式的恆等變形
- 地位:解題的有力手段之一
- 用途:因式分解
概述
幾何學的觀點
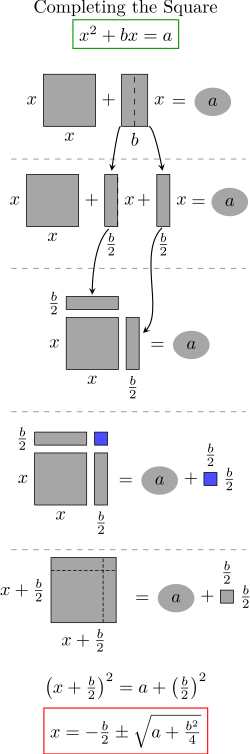
















配方法是指將一個式子(包括有理式和超越式)或一個式子的某一部分通過恆等變形化為完全平方式或幾個完全平方式的和,這種方法稱之為配方法。這種方法常常被用到...
a^2+ 2b^2 解: a^2+2b^2 = a^2+ b^2 + b^2 +2ab-2ab = ( a^2+ b^2 +2ab)-2ab+ b^2 = (a+b)^2-2ab+ b^2 這就是配方法了...
數學方法即用數學語言表述事物的狀態、關係和過程,並加以推導、演算和分析,以形成對問題的解釋、判斷和預言的方法。所謂方法,是指人們為了達到某種目的而採取的手段...
剛體在重力作用下,繞旋轉對稱軸上的定點轉動(拉格朗日陀螺)的歐拉動力學方程的解,對三體問題的求解方法有重要貢獻,解決了限制性三體運動的定型問題。拉格朗日對流體...
的形式,再利用直接開平方法求解的方 圖1配方法解一元二次方程實例 法 [6] [5] 。(1)用配方法解一元二次方程的步驟:①把原方程化為一般形式;②...
解一元二次方程的一種方法,也指套用公式計算某事物。另外還有配方法、十字相乘法、直接開平方法與分解因式法。公式表達了用配方法解一般的一元二次方程的結果。...
因式分解配方法 對於某些不能利用公式法的多項式,可以將其配成一個完全平方式,然後再利用平方差公式,就能將其因式分解,這種分解因式的方法叫做配方法。屬於拆項、...
解一元二次方程的基本思想方法是通過“降次”將它化為兩個一元一次方程。一元二次方程有四種解法: 1、直接開平方法;2、配方法;3、公式法;4、分解因式法。...
完全一元二次方程配方法 將方程配成(x+m)²=n的形式,再利用直接開平方法求解的方法。用配方法解方程的步驟:①把原方程化為一般形式;②方程兩邊同除以二次項...
國中歷史的學習方法HOT百度數說發布中國城市活力報告 內容均由網友貢獻,中文百科無任何收費代編服務 中文百科吧 意見反饋 權威合作 百科協定 詞條...
