基本介紹
研究歷史


 花拉子米
花拉子米 韋達
韋達定義


求根方法
一般方法








求根公式法






圖像法

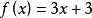


方程套用
基本套用

問題舉例










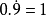
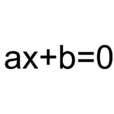


 花拉子米
花拉子米 韋達
韋達
















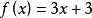













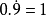
一元一次方程指只含有一個未知數、未知數的最高次數為1且兩邊都為整式的等式。一元一次方程只有一個根。一元一次方程可以解決絕大多數的工程問題、行程問題、分配...
一次方程也被稱為線性方程,因為在笛卡爾坐標繫上任何一個一次方程的表示都是一條直線,因此組成一次方程的每個項必須是常數或者是一個常數和一個變數的乘積,且方程...
1、從形式上看:一次函式y=kx+b,一元一次方程ax+b=0。2、從內容上看:一次函式表示的是一對(x,y)之間的關係,它有無數對值;一元一次方程表示的是未知數x...
線性方程也稱一次方程式。指未知數都是一次的方程。其一般的形式是ax+by+...+cz+d=0。線性方程的本質是等式兩邊乘以任何相同的非零數,方程的本質都不受影響。...
含有兩個未知數,並且含有未知數的項的次數都是1的整式方程叫做二元一次方程。所有二元一次方程都可化為ax+by+c=0(a、b≠0)的一般式與ax+by=c(a、b≠0)...
一元一次不等式是一個數學算式,類似於一元一次方程,含有一個未知數,未知數的次數是1,未知數的係數不為0,左右兩邊為整式的不等式,叫做一元一次不等式。...
《X的一元一次方程組》是連載於幻俠小說的網路小說,作者是陌路鳶。...... 《X的一元一次方程組》是連載於幻俠小說的網路小說,作者是陌路鳶。中文名 X的一元一...
認識二元一次方程組的概念:一些把簡單實際的問題中的數量關係,用二元一次方程組的形式來計算,學會用含有其中一個未知數的代數式表示另一個的方法,成立於一元一次...
一元方程(monadic equation)是一種最簡單的方程,指含有一個未知數的方程,更確切的意義是:如果一個方程中,有若干個字母,當把其中某一個字母當成未知數,而把其餘...
完全一元二次方程是一類簡單的代數方程,即具有標準形式且一次項係數與常數項均不為零的一元二次方程。當一次項係數與常數項至少有一個為零時則稱為不完全一元...
一元一次多項式是最簡單的一種多項式。只含一個變數字母且各項最高次數為1的多項式稱為一元一次多項式。它的標準形式是ax+b(a≠0),式中a,b為常數。...
一元n次方程(equation of degree n with one unknown)是一元n次多項式所確定的方程,指方程a0xn+a1xn-1+…+an=0 (a0≠0),當n≥3時,稱為高次方程.研究...
只含有一個未知數(一元),並且未知數項的最高次數是2(二次)的整式方程叫做一元二次方程。一元二次方程經過整理都可化成一般形式ax²+bx+c=0(a≠0)。...
只含有一個未知數(即“元”),並且未知數的最高次數為3(即“次”)的整式方程叫做一元三次方程(英文名:one variable cubic equation)。一元三次方程的標準形式...
求方程的解的過程稱為“解方程”。 通過方程求解可以免去逆向思考的不易,直接正向列出含有欲求解的量的等式即可。方程具有多種形式,如一元一次方程、二元一次方程...
如果方程組中含有三個未知數,每個方程中含有未知數的項的次數都是一,並且方程組中一共有兩個或兩個以上的方程,這樣的方程組叫做三元一次方程組。常用的未知數有...
三元一次方程是含有三個未知數並且未知數的的項的次數都是1的方程,也就是含有3個未知數的一次方程,其一般形式為ax+by+cz=d。由多個一元一次方程組成並含有三...
二元一次方程是指含有兩個未知數(x和y),並且所含未知數的項的次數都是1的方程。兩個結合在一起的共含有兩個未知數的一次方程叫二元一次方程組。每個方程可...
解一元二次方程的基本思想方法是通過“降次”將它化為兩個一元一次方程。一元二次方程有四種解法: 1、直接開平方法;2、配方法;3、公式法;4、分解因式法。...
一元一次方程只含有一個未知數,且含有未知數的最高次項的次數是一的等式,叫一元一次方程。通常形式是ax+b=0(a,b為常數,且a≠0)。一元一次方程屬於整式方程...
一元四次方程求根公式,是數學代數學基本公式,由義大利數學家費拉里首次提出證明。一元四次方程是未知數最高次數不超過四次的多項式方程,套用化四次為二次的方法,...
結合解法1和解法2,啟發總結出求解像這樣的一元一次方程時,它的移項規律是什麼。(一般地,把含有未知數的項移到一邊,不含未知數的項移到另一邊),習慣上多把含有...
