圖象性質
三次函式性態的五個要點
⒈三次函式y=f(x)在(-∞,+∞)上的
極值點的個數
 三次函式圖象和性質A
三次函式圖象和性質A三次函式的對稱中心
1.三次函式有對稱中心的證明
證明:
因為f(x)=a(x-x0)
3+b(x-x0)+y0的對稱中心是
,即
所以f(x)=ax
3+bx
2+cx+d如果能寫成f(x)=a(x-x
0)3+b(x-x
0)+y
0那么三次函式的對稱中心就是
。
所以設f(x)=a(x+m)3+p(x+m)+n
得f(x)=ax3+3amx2+(3am2+p)x+am3+pm+n
所以3am=b; 3am2+p=c; am3+pm+n=d;
所以m=b/3a; p=(3ac-b2)/3a; n=d+(2b3)/(27a2)-bc/(3a)
所以f(x)=a(x+b/3a)3+(c-B2/3a)(x+b/3a)+d+2b3/27a2-bc/3a
得證。
2.推廣
如果f(x)是一個n次
多項式,n>=2(因為直線的對稱中心從
狹義上講是沒有對稱中心 而在
廣義上講是無數個
對稱中心),其
次項
係數是
,
次項
係數是
,則有
 三次函式圖象A
三次函式圖象A⑴:如果y=f(x)的圖像是
中心對稱圖形,其對稱中心是(-a1/n/a
0,f(-a1/n/a
0));
⑵:如果y=f(x)的圖像是
軸對稱圖形,其對稱軸是x=-a1/n/a
0.
極值計算
三次函式
,其導數為
。易證當
有兩個不相等的實數根時,f(x)具有極大值和極小值。而當
有兩個相等的實數根或沒有實數根時,f(x)不具有極值。
若f(x)有極值,設在
和
處取得,則滿足關係式
,因此以下用
來介紹兩種求三次函式極值的方法。
代入原方程法
該方法為高中學生必須掌握的方法,即通過解方程
,將所得解x
1與x
2代入f(x)中得到極值。
該方法簡潔明了,但存在一個問題,即如果解出來的x1與x2十分複雜(如含有根式,或數字較大等),代入f(x)中計算乘方將是一件不容易的事。下一種方法則可以較好地解決上述問題。
分解因式法
該方法與方法一有重合的地方,都是先求導,計算導數零點x1與x2,但接下來的步驟與方法一有區別。
第二步,計算
。因f(x)是三次多項式,而f'(x)是二次多項式,根據多項式的除法運算法則,商一定是一次多項式,而餘式也是一次多項式(若餘式為常數則無極值)。
不妨設
,因為我們要計算f(x
1)與f(x
2),我們把x
1與x
2代入等號右邊的式子中,再考慮到
,立刻可以得到極值
。這樣一來無論x
1與x
2有多複雜,都可以避免乘方運算,減少錯誤。同時我們可以看到,如果
的餘式僅僅為常數q,那么就有
,因此極值不存在。
與方法一相比,雖然多了
多項式除法這一步,但數字的計算得到了簡化。
零點求法
盛金公式法
三次方程套用廣泛。用根號
解一元三次方程,雖然有著名的卡爾丹公式,並有相應的判別法,但使用卡爾丹公式解題比較複雜,缺乏
直觀性。我國數學家、高中教師範盛金推導出一套直接用a、b、c、d表達的較簡明形式的
一元三次方程的
一般式新求根公式,並建立了新判別法。
1.盛金公式
一元三次方程aX3+bX2+cX+d=0,(a,b,c,d∈R,且a≠0)
當A=B=0時;
當Δ=B2-4AC>0時;
其中,當Δ=B2-4AC=0時;
當Δ=B2-4AC<0時;(詳細見圖)
其中 , (A>0,-1<T<1)。
2.盛金判別法
當Δ=
B2-4
AC>0時,方程有一個實根和一對
共軛虛根。
當Δ=
B2-4
AC=0時,方程有三個實根,其中有一個二
重根。
當Δ=B2-4AC<0時,方程有三個不相等的實根。
3.盛金定理
當
b=0,
c=0時,
盛金公式1無意義;當
A=0時,盛金公式3無意義;當
A≤0時,盛金公式4無意義;當
T<-1或
T>1時,盛金公式4無意義。
當b=0,c=0時,盛金公式1是否成立?盛金公式3與盛金公式4是否存在A≤0的值?盛金公式4是否存在T<-1或T>1的值?盛金定理給出如下回答:
盛金定理1:當A=B=0時,若b=0,則必定有c=d=0(此時,方程有一個三重實根0,盛金公式1仍成立)。
盛金定理2:當
A=
B=0時,若
b≠0,則必定有
c≠0(此時,適用盛金公式1解題)。
 盛金公式1
盛金公式1盛金定理3:當A=B=0時,則必定有C=0(此時,適用盛金公式1解題)。
盛金定理4:當A=0時,若B≠0,則必定有Δ>0(此時,適用盛金公式2解題)。
盛金定理5:當A<0時,則必定有Δ>0(此時,適用盛金公式2解題)。
盛金定理6:當Δ=0時,若A=0,則必定有B=0(此時,適用盛金公式1解題)。
盛金定理7:當Δ=0時,若B≠0,盛金公式3一定不存在A≤0的值(此時,適用盛金公式3解題)。
盛金定理8:當Δ<0時,盛金公式4一定不存在A≤0的值。(此時,適用盛金公式4解題)。
盛金定理9:當Δ<0時,盛金公式4一定不存在T≤-1或T≥1的值,即T出現的值必定是-1<T<1。
注意:盛金定理的
逆定理不一定成立。如:當Δ>0時,不一定有
A<0。
盛金定理表明:盛金公式始終保持有意義。任意實係數的一元三次方程都可以運用盛金公式直觀求解。
卡爾丹公式法
此外,一元三次方程的求根公式用通常的
演繹思維是作不出來的,用類似解一元二次方程的求根公式的配方法只能將型如
ax3+
bx2+
cx+
d=0的標準型一元三次方程形式化為
x3+
px+
q=0的特殊型。
上世紀80年代,中國的一名中學數學教師範盛金對解一元三次方程問題進行了深入的研究和探索,發明了比卡爾丹公式更實用的新求根公式——盛金公式,並建立了簡明的、直觀的、實用的新判別法——盛金判別法,同時提出了盛金定理,盛金定理清晰地回答了解三次方程的疑惑問題,且很有趣味。
 三次函式特殊型的圖象
三次函式特殊型的圖象盛金公式的特點是由
最簡重根判別式A=b2-3ac;B=bc-9ad;C=c2-3bd和總根的判別式Δ=B2-4AC來構成,體現了數學的
有序、
對稱、
和諧與簡潔美,簡明易記、
解題直觀、準確高效,特別是當Δ=B
2-4AC=0時,盛金公式3:X⑴=-b/a+K;X⑵=X⑶=-K/2,其中K=B/A,(A≠0),其表達式非常漂亮,不存在開方(此時的卡爾丹公式仍存在
開立方),手算解題效率高。盛金公式3被稱為超級簡便的公式。
盛金公式與
判別法及定理形成了一套完整的、簡明的、實用的、具有
數學美的解三次方程的理論體系,范盛金創造出的這套萬能的系統方法,對研究解
高次方程問題及提高解三次方程的效率作出了貢獻。
一元三次方程的求解公式的解法只能用歸納思維得到,即根據
一元一次方程、
一元二次方程及特殊的高次方程的求根公式的形式歸納出一元三次方程的求根公式的形式。歸納出來的形如 x
3+px+q=0的一元三次方程的求根公式的形式應該為x=A(1/3)+B(1/3)型,即為兩個開立方之和。歸納出了一元三次方程求根公式的形式,下一步的工作就是求出開立方里的內容,也就是用p和q表示A和B。
方法如下:
⑴將x=A1/3+B1/3兩邊同時立方可以得到
⑵x3=(A+B)+3(AB)1/3(A1/3+B1/3)
⑶由於x=A
1/3+B
1/3,所以⑵可化為 x
3=(A+B)+3(AB)
1/3x,
移項可得
⑷x
3-3(AB)
1/3x-(A+B)=0,和一元三次方程和特殊型x
3+px+q=0
作比較,可知
⑸-3(AB)
1/3=p,-(A+B)=q,
化簡得
⑹A+B=-q,AB=-(p/3)3
⑺這樣其實就將一元三次方程的求根公式化為了一元二次方程的求根公式問題,因為A和B可以看作是一元二次方程的兩個根,而⑹則是關於形如ay
2+by+c=0的一元二次方程兩個根的
韋達定理,即
⑻y1+y2=-(b/a),y1*y2=c/a(韋達定理)
⑼對比⑹和⑻,可令A=y1,B=y2,q=b/a,-(p/3)3=c/a
⑽由於形為ay2+by+c=0的一元二次方程求根公式為
y1=-(b+(b2-4ac)1/2)/(2a)
y2=-(b-(b2-4ac)1/2)/(2a)
可化為⑾y1=-(b/2a)-((b/2a)2-(c/a))1/2
y2=-(b/2a)+((b/2a)2-(c/a))1/2
將⑼中的A=y1,B=y2,q=b/a,-(p/3)3=c/a代入⑾可得
⑿A=-(q/2)-((q/2)2+(p/3)3)1/2
B=-(q/2)+((q/2)2+(p/3)3)1/2
⒀將A,B代入x=A1/3+B1/3得
⒁x=(-(q/2)-((q/2)2+(p/3)3)1/2)1/3+(-(q/2)+((q/2)2+(p/3)3)1/2)1/3
式 ⒁只是一元三方程的一個實根解,按韋達定理一元三次方程應該有三個根,不過按韋達定理一元三次方程只要求出了其中一個根,另兩個根就容易求出了。
其他性質
特殊性質;在高考中的套用;三次函式的三大性質。
 三次函式圖象和性質A
三次函式圖象和性質A
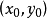


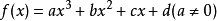

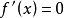
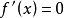







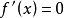



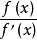



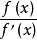
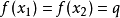




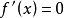



 盛金公式1
盛金公式1 三次函式特殊型的圖象
三次函式特殊型的圖象
 三次函式圖象和性質A
三次函式圖象和性質A
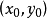


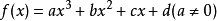

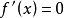
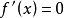







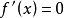



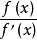



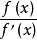
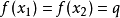




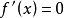



 盛金公式1
盛金公式1 三次函式特殊型的圖象
三次函式特殊型的圖象