基本介紹
- 中文名:n次單位根
- 外文名:n-th unit root
- 所屬學科:數學
- 所屬問題:初等代數(數系)
- 簡稱:單位根
- 簡介:數1在複數範圍內的n次方根
基本介紹
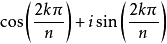
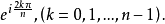
n次單位根的性質
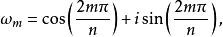
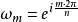
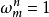
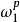
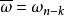

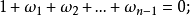
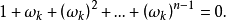
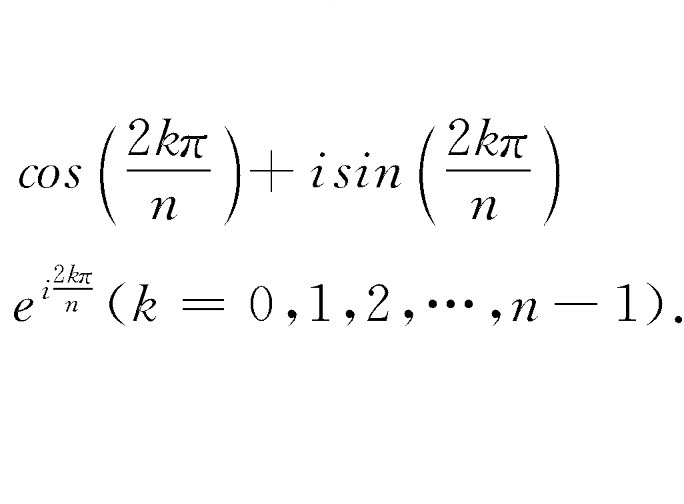
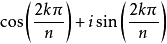
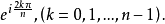
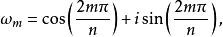
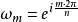
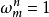
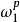
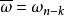

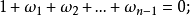
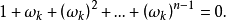
n次單位根(n-th unit root)是一種重要的n次方根,數1在複數範圍內的n次方根,稱為n次單位根,簡稱單位根。由此可知,所謂n次單位根,也就是多項式xn-1或方程...
數學上,n次單位根是n次冪為1的複數。它們位於複平面的單位圓上,構成正n邊形的頂點,其中一個頂點是1。...
如果一個數的n次方(n是大於1的整數)等於a,那么這個數叫做a的n次方根。習慣...不能無歧義的使用。n次單位根是特別重要的。當一個數從根號形式被變換到冪形式...
在數學中,若一個數b為數a的n次方根,則bn=a。如果n是偶數,那么負數將沒有...不能無歧義的使用。n次單位根是特別重要的。當一個數從根號形式被變換到冪形式...
分圓多項式是指某個n次本原單位根滿足的最小次數的首1的整係數多項式(它必定是不可約多項式)。...
,它們被稱做 n 次單位根,具體可以寫作: 。在ℚ中添加 得到的擴域稱為 n 次分圓域,記作 。可以證明 是有限維ℚ-向量空間,維數為 (φ是數論中的歐拉函...
群G=G(E/F)中元素的最大階數為m(m稱為G的指數),並且F含m個不同的m次單位根,則E稱為F的庫默爾m擴張;E稱為庫默爾域,例如,設F含本原n次單位根,且E...
對有理數域Q添加一個本原n次單位根ξ所得的分圓擴張Q(ξ)稱為圓的n分域,它是有理數域Q的φ(n)次阿貝爾擴域,其中φ(n)為歐拉函式。n分域來源於...
特別,由於 為n次單位根。故由此即得下述引理。引理1 設n為奇數,1≤i≤4,1≤j≤(n-1)/2,若滿足定理3條件的循環矩陣 存在,則其係數tij必滿足式9)。...
分圓域擴張(cyclotomic field extension)一類重要的阿貝爾擴張.設門是域F的代數閉包,其中間域K稱為F的一個分圓擴域,若K是通過對F添加某些單位根而生成的。...
