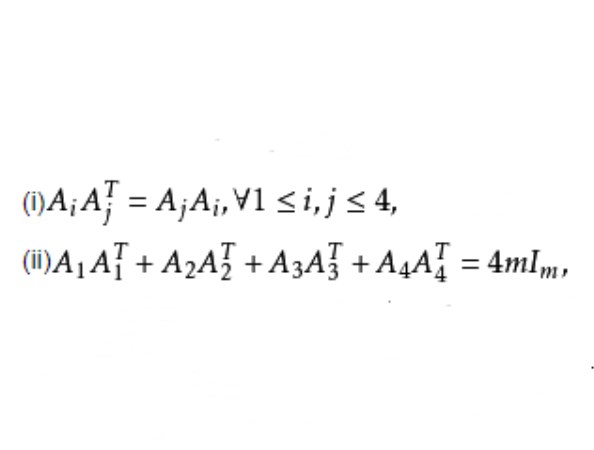威廉森型矩陣(Williamson matrix)是一組特殊的矩陣，其元素為±1，元素為±1的4個m階矩陣A，B，C，D，若滿足AAT+BBT+CCT+DDT=4mI，且對其中的任兩個矩陣M，N均有MNT=NMT，則稱它們為威廉森型矩陣，這類矩陣是因為遞推構造H矩陣的需要而提出的，若存在m階威廉森型矩陣且存在t階鮑默特-霍爾表，則存在4mt階H矩陣，當q為模4餘1的質數冪時，存在(q+1)/2階及q(q+1)/2階的威廉森型矩陣，對於階數不大於29的奇數及其他較小的階數，存在威廉森型矩陣。
基本介紹
- 中文名：威廉森型矩陣
- 外文名：Williamson matrix
- 所屬學科：數學
- 所屬問題：組合學（組合設計理論）
- 簡介：一組特殊的矩陣
基本介紹,相關性質定理,
基本介紹
定義 設A1，A2，A3，A4為4個m階(1，-1)-矩陣，若以下條件滿足：
(i)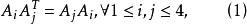
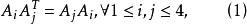
(ii)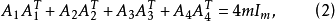
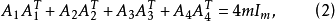
則稱{A1，A2，A3，A4}為一組m階威廉森型矩陣(Williamson型矩陣,Williamson-type matrix)。
定義 設{A1，A2，A3，A4}為4個滿足條件(2)的m階對稱循環(1,-1)-矩陣。則稱{A1，A2，A3，A4}為一組m階威廉森(Williamson)矩陣。
由於n階循環矩陣都能表成U的多項式。因此任意一對n階循環矩陣Ai與Aj必可交換即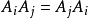
．從而Williamson矩陣必滿足條件(1)，亦即Williamson矩陣必為Williamson型矩陣。
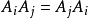
相關性質定理
定理1(Geramita-Seberry)設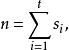
若存在OD(n；s1，s2，...，st)及它的一組m階適配矩陣{A1，A2，...，At},則存在mn階H-陣。
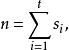
定理2 若OD(4s；s,s,s,s)與m階Williamson型矩陣都存在，則4ms階H-陣也必存在。
證明由定義知，Williamson型矩陣是Baumert-Hall陣列的適配矩陣，從而由定理1即得結論。
下面是Williamson矩陣和Williamson型矩陣的構作方法。
定理3(Williamson)設n為奇數，U為如下所給出的n階循環矩陣
若存在4個如下形狀的n階對稱循環矩陣：
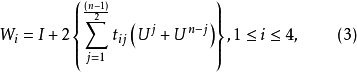
(i)對任意1≤i≤4,1≤j≤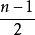
,都有
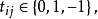並且對任一j,1≤j≤ ,
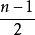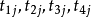中都恰有一個為±1,其餘3個均為0,
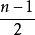
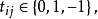
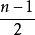
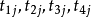
(ii)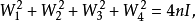
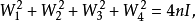
則存在佗階Williamson矩陣{A1，A2，A3，A4}。
上述定理把尋求Williamson矩陣的問題轉化為尋求滿足定理條件的矩陣組{W1，W2，W3，W4}的問題。
n階循環矩陣U的特徵多項式為
式（4）因此U有n個不同的特徵根。從而存在n×n非奇異陣P使
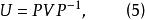
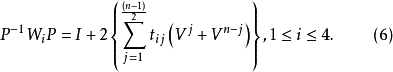
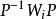
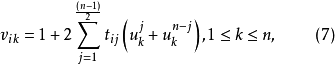
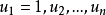
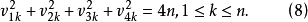
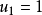
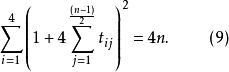
引理1 設n為奇數，1≤i≤4，1≤j≤(n-1)/2,若滿足定理3條件的循環矩陣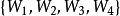
存在,則其係數tij必滿足式9)。
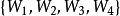
因此為構作Wi，1≤i≤4，首先將4n表為4個奇數的平方和，然後尋求滿足條件的諸係數tij。
引理2 設n為奇數，則4n必可表為4個奇數的平方和。
藉助於引理1與2，可以在很大程度上減少尋找Wi的工作量，不過即便如此，當n較大時，構作Williamson矩陣仍非易事。
Williamson方法的一個成功套用是Baumert，Golomb與Hall於1962年用以給出23階Williamson矩陣的構作，從而證明了92階Hadamard矩陣的存在性，我們把這一結果整理在下述引理中。
引理3 設n=23，29，39或43，則n階Williamson矩陣存在，從而4n階H-陣也存在。
夏明遠與劉剛給出的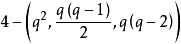
差族與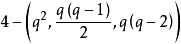差族，構造了兩類Williamson型矩陣。
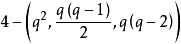
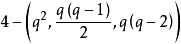
定理4(Xia，Liu)若q為素數冪，q≡1(mod 4)，則存在q2階Williamson型矩陣。
定理5 (Xia，Liu)設q為素數冪，q≡3(mod 8)，則存在q2階Williamson型矩陣。
由定理4定理5及定理2即得下述定理。
定理6(Xia，Liu)若q為素數冪，q≡1(mod 4)或q≡3(mod 8)，則4q2階Hadamard矩陣存在。
