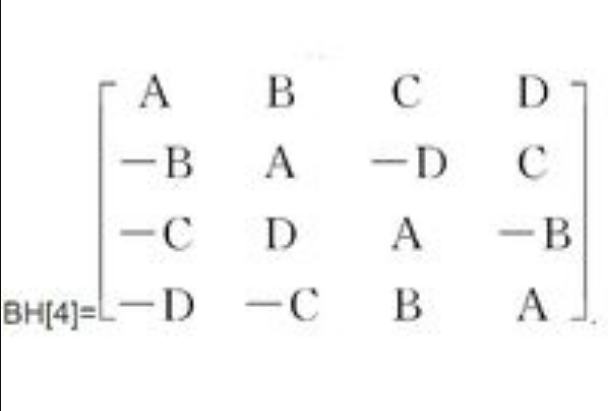
鮑默特-霍爾表(Baumert-Hall array)亦稱鮑默特-霍爾陣列、Baumert-Hall陣列,是阿達馬矩陣的推廣,因遞推構造阿達馬矩陣而提出,若元素為未定元±A,±B,±C,±D的4t階矩陣的每一行及每一列含每個未定元X(包括-X)各t次,並且把A,B,C,D看做可換環中元素時每兩行都是正交的,則稱該矩陣為t階鮑默特-霍爾表,記為BH[4t],若存在t階的鮑默特-霍爾表BH[4t],且存在m階的威廉森型矩陣,則存在4mt階的H矩陣.該H矩陣可將BH[4t]中的未定元A,B,C,D換作4個威廉森型矩陣而得到,若取A=B=C=D=1,則從一個BH[4t]得到一個4t階的H矩陣,當t=1+2a10b26c,a,b,c為非負整數時,存在BH[4t],當t為不大於33的奇數或其他一些奇數時,也存在BH[4t]。
基本介紹
- 中文名:鮑默特-霍爾表
- 外文名:Baumert-Hall array
- 別稱:Baumert-Hall陣列
- 所屬學科:數學
- 所屬問題:組合數學(組合設計理論)
- 簡介:阿達馬矩陣的推廣
基本介紹









鮑默特-霍爾表的構作方法
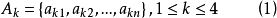

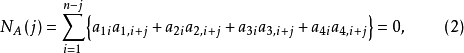
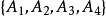
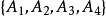
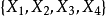
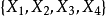
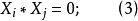
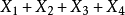
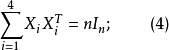
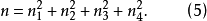
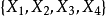
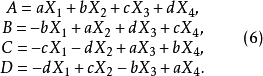
 式(7)
式(7) 式(8)
式(8)