基本介紹
- 中文名:阿達馬矩陣
- 外文名:hadamard matrix
- 範疇:數學
- 提出者:阿達瑪
- 類型:矩陣中的方陣
- 套用學科:數學
性質


西爾維斯特構造法



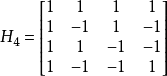
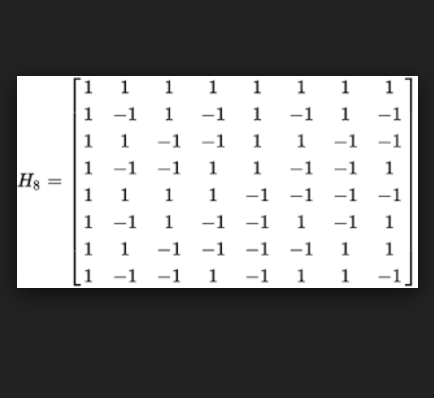





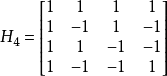
在數學中,阿達馬矩陣是一個方陣,每個元素都是 +1 或 −1,每行都是互相正交的。阿達馬矩陣常用於糾錯碼,如Reed-Muller碼。阿達馬矩陣的命名來自於法國數學家...
阿達馬碼(Hadamard code)是一種重要的碼,它是從阿達馬矩陣產生的二元碼,設Hn是一個n階阿達馬矩陣,用0代替Hn與-Hn中的元素-1,這樣可得2n個行,它們都是Fn2...
正規阿達馬矩陣是一個數學原理。...... 正規阿達馬矩陣(regular Hadamard matrix)一類特殊的阿達碼矩陣.其行和為常數.這類矩陣每行所含1的個數都相同.當4n階正...
阿達馬設計(Hadamard design)是一類特殊參數的對稱設計,即(4t-1,2t-1,t-1)-SBIBD。當4t階H矩陣存在時,經交換兩行、交換兩列、某行乘以-1、某列乘以-1...
復阿達馬矩陣(complex Hadamard matrix )阿達馬矩陣的推廣.設n階復矩陣C的元素為士1或士i,若CC' =nl ,則稱C為復阿達馬矩陣,這裡C‘是C的厄米特共扼矩陣,...
反型阿達馬矩陣(skew Hadamard matrix)一類特殊阿達馬矩陣.若一個阿達馬矩陣與單位矩陣的差是反對稱矩陣,則稱這個阿達馬矩陣為反型的.這一概念是為了遞推構造H...
廣義阿達馬矩陣(generalized Hadamard ma-trix)阿達馬矩陣的推廣.設H=H(p}n)是元素為p次復單位根的n階矩陣,若滿足HH * =nl>,,則稱H為廣義阿達馬矩陣.H(...
阿達馬矩陣睦偶(amicable Hadamard matrix )特殊的阿達馬矩陣對,設M是一個反型H矩陣,N是一個同階的對稱H矩陣,若它們適合等式MNT = NMT,則稱它們是一對阿達馬...
對稱C矩陣(symmetric conference matrix)與阿達馬矩陣有關的一類矩陣,若元素為士1的n階對稱矩陣C的對角線元均為1且適合等式(C一1)2= <n一1>1,則稱C為對稱...
在計算數學中,一個與阿達馬變換有高度相關的快速沃爾什轉換(fast Walsh–Hadamard transform,FWHTh)是一個十分有效率的算法,目的是計算阿達馬變換。快速沃爾什轉換是...
他還與人合作 在用伽羅瓦理論構造阿達馬矩陣方面得到了現已知 的三類會議矩陣(Conference matrices)族中的一 個,發現了D最佳設計中的第二個族,並在與差集 相關的...
。這個門可以以阿達馬矩陣表示:因因為矩陣的每一列正交,因此H 是一個酉矩陣。量子門泡利-X 門 泡利-X 門操作一個量子比特。 這個門相當於經典的邏輯非門。 它...
量子非門阿達馬門(Hadamard gate) 阿達馬門是只對一個一個量子比特進行操作的門。 這個門將基本狀態 變成 ,並且將 變成 。這個門可以以阿達馬矩陣表示:...
矩陣的阿達馬乘積 矩陣的克羅內克乘積 張量的外積 張量的張量積 兩個函式的逐點乘積 就代數結構而言有:笛卡兒積 向量空間的直積 群子集的乘積 群的...
18.二次互反律【n角形數與費爾馬】19.雅可比符號【阿達馬矩陣和猜想】20.合數模同餘【正十七邊形作圖法】伍n次剩餘21.指數的定義【埃及分數】...
3.布局,包括正交拉丁方、區組設計、正交表、阿達馬矩陣、差集等.經典組合學常討論以下三個問題,即特定安排的存在性問題、特定安排的計數間題和尋求在某個最佳化準則...
4.4 雅可比符號【阿達馬矩陣和猜想】 4.5 合數模同餘【正十七邊形作圖法】 習題 第五章 原根與n次剩餘 5.1 指數的定義【埃及分數】 5.2 原根的存在...
3.5.2阿達馬矩陣法943.5.3正交拉丁方的方法973.5.4混合型正交表構造法1013.6正交試驗設計的方差分析1083.6.1正交設計方差分析的步驟與格式108...
(0,1)-矩陣第17章 拉丁方第18章 阿達馬矩陣和里德米勒碼第19章 設計第20章 碼和設計第21章 強正則圖和部分幾何第22章 正交拉丁方第23章 射影幾何和組合...
某些對稱設計可用來構作阿達馬矩陣,另一些可用來構作雙偶自對偶碼。 [1] 對稱平衡不完全區組設計平衡不完全區組設計 編輯 (balanced incomplete block design)...
