在計算數學中，一個與阿達馬變換有高度相關的快速沃爾什轉換（fast Walsh–Hadamard transform，FWHTh）是一個十分有效率的算法，目的是計算阿達馬變換。快速沃爾什轉換是一個分而治之的算法，是一個常見的遞迴方法，將大小N的沃爾什轉換拆成兩個大小為N/2 的沃爾什轉換。
基本介紹
- 中文名：快速沃爾什轉換
- 外文名：fast Walsh–Hadamard transform
- 學科：計算數學
- 目的：計算阿達馬變換
- 算法類型：分而治之
- 有關術語：沃爾什轉換
簡介,沃爾什轉換,阿達馬變換,
簡介
快速沃爾什轉換是一個用於計算阿達馬變換的方法。一個直觀且基本的沃爾什轉換，他的計算複雜度 大約是 O(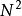
)。而快速沃爾什轉換隻需要
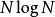個加法或是減法即可。根據 
阿達馬矩陣
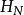的遞迴定義：
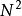
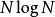
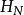
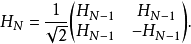
其中
的正規化項可以提出或省略掉。
沃爾什矩陣，又叫沃爾什序列，快速沃爾什轉換FWHTw，就是用上面的作法計算以後，把輸出結果排成序列。快速沃爾什轉換在諸如圖象處理等領域中有重要的套用價值，而在這些套用領域，待處理的數據量特別大，又常常有實時處理的要求。
沃爾什轉換
沃爾什轉換（Walsh Transform）是在頻譜分析上作為離散傅立葉變換的替代方案的一種方法。
在頻譜分析上最常用的一種方法是使用離散傅立葉變換，然而，即使已經有許多快速的算法來實現離散傅立葉變換，仍然具有一些實現上的缺點，舉例來說，在離散傅立葉變換中，資料向量必須乘上複數係數的矩陣加以處理，而且每個複數係數的實部和虛部是一個正弦及餘弦函式，因此大部分的係數都是浮點數，也就是說在做離散傅立葉變換處理的時候，我們必須做複數而且是浮點數的運算，因此計算量會比較大，而且浮點數運算產生的誤差會比較大。
而在沃爾什轉換中，資料向量需要乘上的矩陣是一個實數的矩陣，而且這些矩陣的係數是1或是–1，因此所有的係數都是絕對值大小相同的整數，這使得我們不需要作浮點數的乘法運算，更進一步，只需要使用加法來實現沃爾什轉換，這使的沃爾什轉換在運算複雜度上遠小於離散傅立葉變換。使用離散傅立葉變換相當於把信號拆解成在不同頻率的正弦函式與餘弦函式的分量，而使用沃爾什轉換相當於把信號拆解成在許多不同震盪頻率的方波上，因此，除非所要分析的信號擁有類似方波組合的特性，使用沃爾什轉換作頻譜分析的效果會比使用離散傅立葉變換分析的效果要差，這是降低運算複雜度所要付出的代價。沃爾什轉換的轉換式為
其中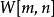 
是沃爾什轉換矩陣的第（m,n）個元素。 舉例來說，一個8點沃爾什轉換的轉換矩陣如下：
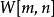
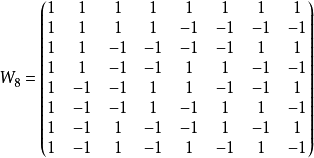
後面會解釋沃爾什轉換矩陣是如何產生，而沃爾什轉換的反轉換式為
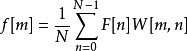
注意到正轉換式與反轉換式只差了一個常數，這是由於沃爾什轉換矩陣的反矩陣就是自己的轉置矩陣乘上一個常數的緣故。
阿達馬變換
阿達馬變換（Hadamard transform），或稱沃爾什-阿達瑪轉換，是一種廣義傅立葉變換（Fourier transforms），作為變換編碼的一種在影片編碼當中使用有很久的歷史。在近來的影片編碼標準中，阿達馬變換多被用來計算SATD(一種影片殘差信號大小的衡量)。在數位訊號處理大型積體電路算法的領域中，阿達馬變換是一種簡單且重要的算法之一，主要能針對頻譜做快速的分析。在H.264中使用了4階和8階的阿達馬變換來計算SATD，其變換矩陣為：
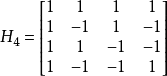
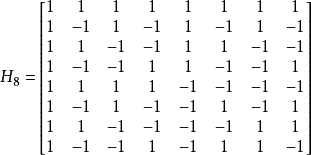
優點
- 僅需實數運算 (Real operation) 。
- 不需乘法運算 (No multiplication) ，僅有加減法運算。
- 有部分性質類似於離散傅立葉變換 (Discrete fourier transform) 。
- 順向轉換 (Forward transform) 與反向轉換 (Inverse transform ) 型式為相似式。
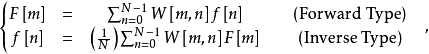
其中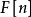
與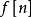
分別都為行向量 (Column vector) 。
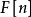
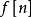
缺點
- 其收斂速度較離散餘弦變換慢，因此對於頻譜分析的效果較差。
- 其加減法量較離散傅立葉變換、離散餘弦變換多。
