基本介紹
- 中文名:默比烏斯變換
- 外文名:Mobius transformation;homographic transformations
- 所屬領域:數理科學
- 別名:默氏變換
- 人物:奧古斯特·費迪南德·莫比烏斯
簡介
複平面中的默比烏斯變換

數論中的默比烏斯變換







定義





分解









性質
保角性與保圓性
複比不變性






確定默比烏斯變換














矩陣表示






















































默比烏斯變換(Mobius transformation),也稱莫比烏斯變換,是數論中的一種重要變換。默比烏斯變換是以數學家奧古斯特·費迪南德·莫比烏斯命名的,它也被叫做homographic transformatio...
雙線性變換是一種特別的共形映射(即莫比烏斯變換),常被用來將線性非時變系統濾波器在連續時域的傳遞函式轉換成線性且平移不變濾波器在離散時域的傳遞函式。將S平面中位置在 軸的點映射到複數平面上的單位圓 。其他的套用還有扭曲任何...
其中μ是Möbius函式,並且和在n的所有正除數d之間延伸。 實際上,原始的f(n)可以通過使用反演公式給出g(n)來確定。 這兩個序列是彼此的莫比烏斯變換。如果f和g是從正整數到某些阿貝爾組(被視為ℤ模組)的函式,那么公式也是...
通過研究,獲得了理想HCP結構的莫比烏斯變換公式及更普遍的非理想HCP結構的莫比烏斯變換公式,從而完善了晶體中的莫比烏斯變換方法。進一步研究了在莫比烏斯變換中如何考慮三體勢及如何確定三體勢的參數。最後獲得了理論計算確定三體勢參數的方法。
.莫比烏斯變換的例子包括膨脹,旋轉,平移,和復倒數。事實上,所有莫比烏斯變換可以有這些特例的複合得到。將莫比烏斯變換視作復射影線上的變換很有益。這樣,莫比烏斯變換可以表述為行列式非零的復矩陣;兩個矩陣產生同樣的莫比烏斯變換當且...
9.1 陳-莫比烏斯變換 9.1.1 引言 9.1.2 莫比烏斯變換 9.1.3 陳-莫比烏斯變換 9.2 晶體中聲子態密度的逆問題 9.2.1 逆變換公式 9.2.2 低溫近似 9.2.3 高溫近似 9.3 晶體內原子間相互作用勢的逆問題 9.3.1 一維...
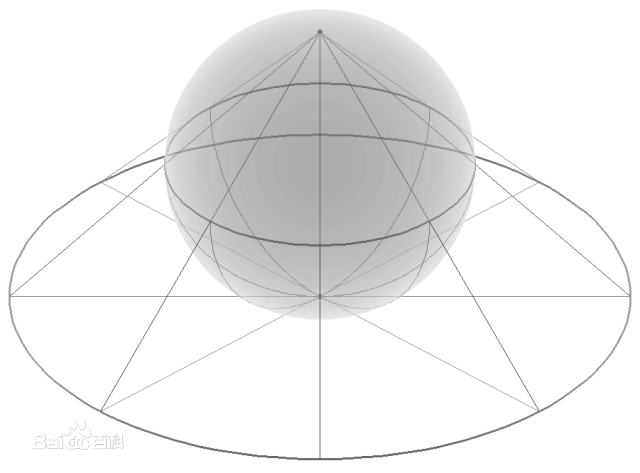
作用於球面上以及作用於球極投影的平面上的莫比烏斯變換。主條目:莫比烏斯變換理解數學對象的自同構群有助於對該對象的研究,自同構也就是對象到自身保持其基本結構不變的映射。對於黎曼球面,自同構就是黎曼球面到自身的可逆雙全純映射。
