默比烏斯反演公式(Mobius inversion formula)一種序列反演公式。經典的莫比烏斯反演公式在十八世紀由費迪南德·莫比烏斯（FerdinandMöbius）引入到數學理論中。在數學上，當不同的局部有限部分有序集合取代了通過可分性排序的自然數的經典情況時，便可獲得其他莫比烏斯反演公式。
基本介紹
- 中文名：默比烏斯反演公式
- 外文名：Mobius inversion formula
- 首創：FerdinandMöbius
- 年份：1832年
- 領域：數學
- 屬性：序列反演公式
簡介,公式聲明,系列關係,重複轉換,推廣,乘法符號,概括證明,
簡介
默比烏斯反演公式(Mobius inversion formula)一種序列反演公式。它是德國數學家默比烏斯(Mobius , A. F.)提出的，最早出現在初等數論的研究中。設f(n)和g(n)是定義在自然數集N上的兩個函式，反演公式：
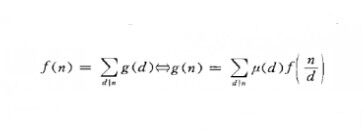
稱為(經典的)默比烏斯反演公式。這裡，記號“拼”表示左右兩式可以互推。函式爪n)是默比烏斯在1832年研究素數分布時首次引入的，後稱它為(經典的)默比烏斯函式。
公式聲明
經典版本說明，如果g和f是算數函式，則：
其中μ是Möbius函式，並且和在n的所有正除數d之間延伸。 實際上，原始的f（n）可以通過使用反演公式給出g（n）來確定。 這兩個序列是彼此的莫比烏斯變換。
如果f和g是從正整數到某些阿貝爾組（被視為ℤ模組）的函式，那么公式也是正確的。
用Dirichlet卷積的語言，第一個公式可以寫成：g=f
1，
其中*表示Dirichlet卷積，1是常數函式1（n）= 1。然後將第二個公式寫為：f=
g。
關於乘法函式的文章中給出了許多具體的例子。
定理遵循因為*是（交換和）關聯，並且1 *μ=ε，其中ε是Dirichlet卷積的同一性函式，對於所有n> 1，取值ε（1）= 1，ε（n）= 0 因此：
系列關係
我們使：
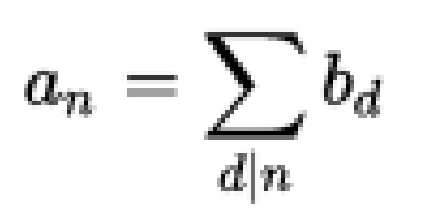
因此得到：
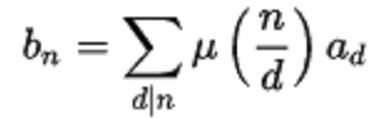
這個式子是它的轉變。 這些變換是通過系列方式進行的，蘭伯特系列：
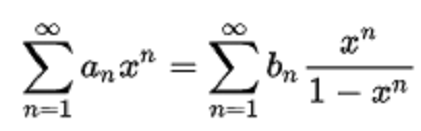
和Dirichlet系列：
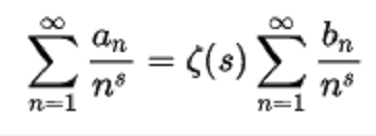
其中ζ（s）是Riemann zeta函式。
重複轉換
給定算術函式，可以通過重複套用第一個求和來生成其他算術函式的雙無限序列。
例如，如果從歐拉的常數函式開始，並重複套用變換過程，則得到：
1.φ的常數函式
2.φ* 1 = I，其中I（n）= n是識別函式
3.I * 1 =σ1=σ，除數函式
如果起始功能是Möbius功能本身，功能列表是：
1.μ，Möbius函式
2.μ* 1 =ε其中，
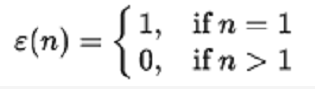
是單位功能。
3.ε* 1 = 1，常數函式
4.1 * 1 =σ0= d =τ，其中d =τ是n的除數，（見除數函式）。
這兩個功能列表在兩個方向都無限延伸。 Möbius反演公式使得這些列表能夠向後遍歷。
作為一個例子，從φ開始的序列是：
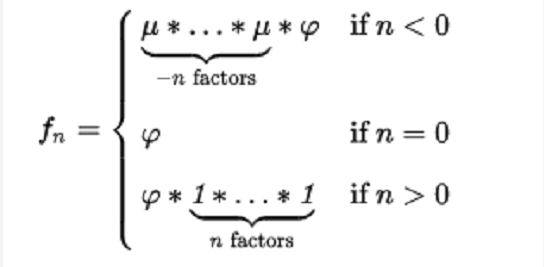
通過考慮相應的Dirichlet系列可以更容易地理解生成的序列：變換的每個重複套用對應於Riemann zeta函式的乘法。
推廣
在組合中更有用的相關反演公式如下：假設F（x）和G（x）是在區間[1，∞）上定義的復值函式，使得：
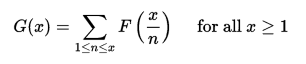
那么：
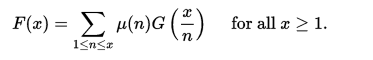
這裡的總和擴展到小於或等於x的所有正整數n。
這反過來又是一個更一般形式的特殊情況。 如果α（n）是具有Dirichlet反
的算術函式，則如果定義：
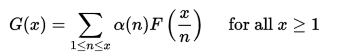
那么：
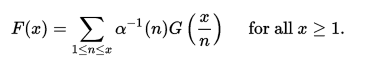
如果我們在正整數上定義（復值）函式f（n）和g（n），則會出現這些擴展中的第一個的特定套用，
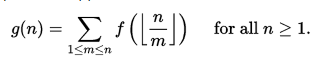
通過定義F（x）= f（⌊x⌋）和G（x）= g（⌊x⌋），我們推導出：
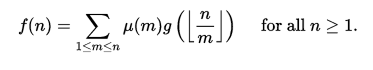
使用此公式的一個簡單示例是計算減少比例0 <
<1，其中a和b是互質的，b≤n。 如果我們令f（n）為這個數字，則g（n）是分數0<<1的總數，其中b≤n，其中a和b不一定是互質的。（這是因為每個分數滿足gcd（a，b）= d和b≤n，並且可以減少到分數
，其中
，反之亦然）。這裡可以直接確定g（n）=
，但是f（n）更難計算。
另一個反演公式是（我們假設所涉及的系列是絕對收斂的）：
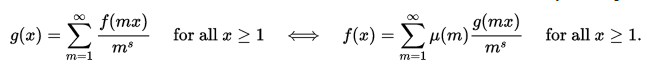
如上所述，這概括為α（n）是具有Dirichlet反α-1（n）的算術函式：
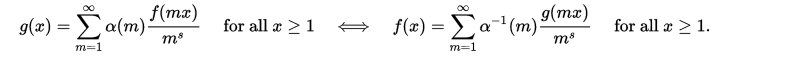
乘法符號
由於Möbius反演適用於任何阿貝爾組，所以組操作是作為加法還是作為乘法來表示沒有區別。 這產生了以下反演公式的符號變體：
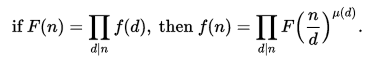
概括證明
第一個概括可以證明如下。 我們使用Iverson的約定，[condition]是條件的指標函式，如果條件為真，則為1，如果為false則為1。我們使用的結果，
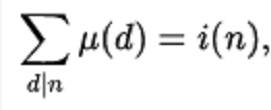
即1 *μ= i。我們可以進行一下證明：
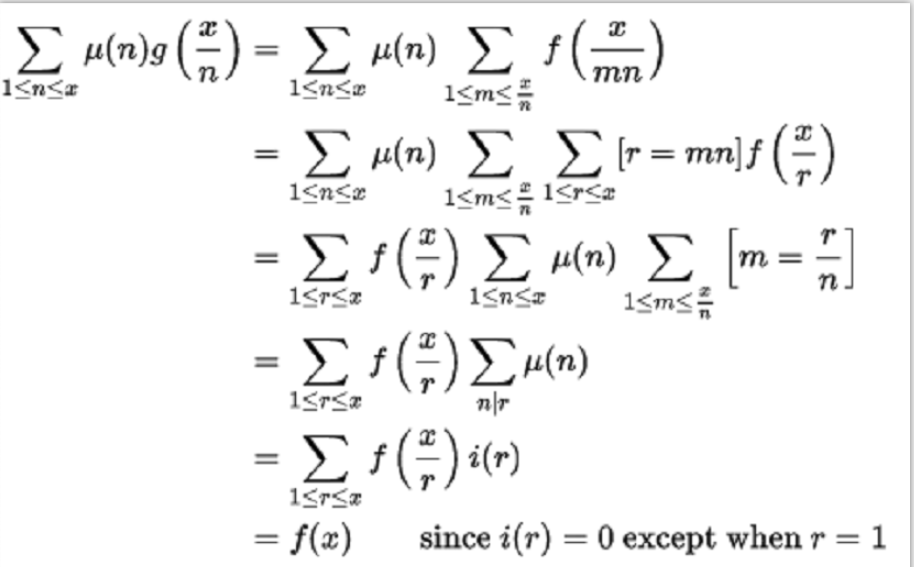
在α（n）代替1的更一般情況下的證明基本上是相同的，如第二次泛化。
