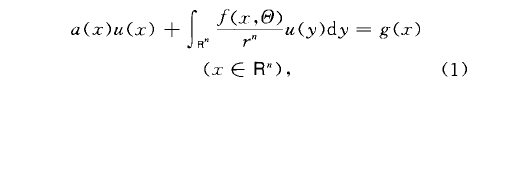
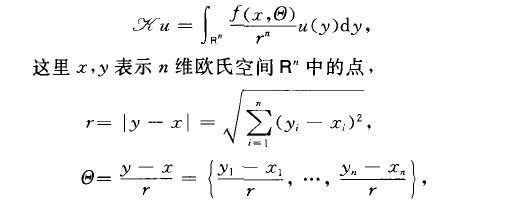
高維奇異積分方程(singular integral equationin high dimension)希爾伯特變換在高維的推廣·與弗雷德霍姆積分方程不同，對於奇異積分方程，高維和一維是需要加以區別的.典型的高維奇異積分方程是指方程其中的奇異積分運算元是研究得最多的考爾德倫一贊格蒙一米赫林奇異積分運算元。
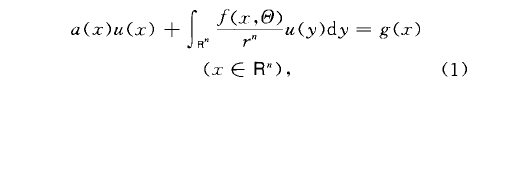
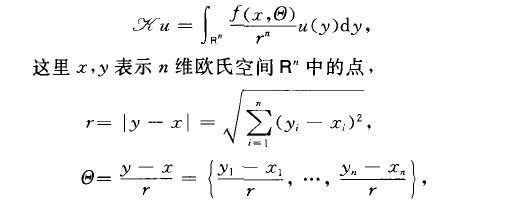
高維奇異積分方程(singular integral equationin high dimension)希爾伯特變換在高維的推廣·與弗雷德霍姆積分方程不同，對於奇異積分方程，高維和一維是需要加以區別的.典型的高維奇異積...
2.以維納-霍普夫方程為代表的帶差核的積分方程；3.對偶積分方程。人們在相當深入地研究了以上幾類奇異積分方程，以及它們相應的離散形式、方程組、高維的情形和各種各樣的推廣以後就企圖用統一的觀點去處理它們。統一的一個途徑是把它們...
即柯西核積分方程、黎曼邊值問題(包括帶位移)、維納一霍普夫方程、對偶積分方程，以及它們相應的離散形式、方程組和高維的推廣，統一的途徑是把它們作為下面的廣義的維納一霍普夫方程的特例.設A,B是希爾伯特空間上的已知的線性運算元.屍是...
柯西奇異積分方程（Cauehy singular integral equations）是一類最基本且具有廣泛實際套用的奇異積分方程，其積分是柯西主值意義下的。柯西奇異積分方程與弗雷德霍姆積分方程之間有著本質的不同。定義 柯西奇異積分方程是一類最基本且具有廣泛...
《Clifford分析理論與高維空間的偏微分方程》是依託河北師範大學，由喬玉英擔任項目負責人的面上項目。項目摘要 研究Clifford分析中超正則函式的性質和超調和函式的性質，研究它們的在有界、無界域上的積分表示及其邊值問題。研究高階奇異積分...
本書可作為計算數學和套用數學專業的博士生、碩士生和本科高年級學生的教材或參考書，也可作為從事積分方程和工程邊界元計算的科研工作者和工程技術人員的參考資料。圖書目錄 第1章奇異積分與青異積分運算元 第2章數值積分 第3章一維奇異...
由於計算複雜度高，高維弱奇異問題的數值方法及加速技術也鮮有涉及。本項目擬利用插值後處理、校正、積分展開式和外推技術，提高線性及非線性弱奇異Volterra積分方程數值解的精度，並分析插值後處理在求解此類方程的優勢；將快速算法與後處理...
我們重點研究線性與非線性第二類帶弱奇異核的Volterra積分方程、帶中立項的弱奇異Volterra型微分積分方程Jacobi、常數延遲、變延遲及比例延遲等多種類型Volterra延遲型積分微分方程、高維區域的 Volterra積分微分方程及分數階微分方程譜配置方法...
《超奇異積分方程數值求解中的超收斂現象研究及其套用》是依託武漢大學，由張曉平擔任項目負責人的數學天元基金項目。項目摘要 超奇異運算元的數值研究是現代邊界元方法中的一個重要研究內容。隨著超奇異積分的套用範圍的不斷拓展，其計算方法的...
《Volterra方程與高維分數階擴散方程的理論與數值研究》是依託福州大學，由李嫻娟擔任項目負責人的青年科學基金項目。項目摘要 本項目擬從理論和數值計算兩方面對 Volterra 積分方程以及高維分數階擴散方程進行深入研究，主要內容包括以下兩個...
對數方程組(system of logarithmic equations)是一種常用的代數方程組，指由幾個對數方程，或至少有一個對數方程和幾個代數方程組成的方程組。解對數方程組的一般步驟是：1.把方程組中的對數方程化為代數方程；2.解代數方程組；3.驗根...
《奇異微分方程邊值問題解的研究》是2017年科學出版社出版的圖書，作者是曹忠威、祖力。內容簡介 非線性奇異微分方程邊值問題與奇異積分方程問題是方程理論中的重要課題，是科學研究和解決技術問題的主要工具，具有廣泛的套用價值，它豐富的...
里斯運算元是一類重要的高維奇異積分運算元。它是指下面的m個運算元 其中 是n維空間Rⁿ的點，性質 里斯運算元是將f∈L²映射到L²的有界運算元，對m=1,2,...,n，它滿足關係式：其中I為恆等運算元。套用 里斯運算元在雙曲型偏微分方程的...
在Clifford分析平台上，研究由Dirac運算元所決定的函式（正則函式、高階正則函式、超復調和函式、高階超復調和函式等）的各類邊值問題以及相關高維超復奇異積分方程的理論和套用。這兩個方面的研究相互影響和促進，互為犄角。前者的成果為後...
近幾十年來, 這類問題也獲得了眾多專家學者的極大關注. 本項目主要研究高振盪Bessel型積分、幾類高振盪奇異積分、多頻高振盪積分以及高維高振盪積分的計算、高振盪奇異積分方程的數值解以及圖像重建中遇到的高振盪問題, 為了克服奇異性和...
