高斯映射是從歐氏空間R3中的一個曲面到單位球面S2的一個映射,以卡爾·弗里德里希·高斯命名。
基本介紹
定義,全曲率,推廣,
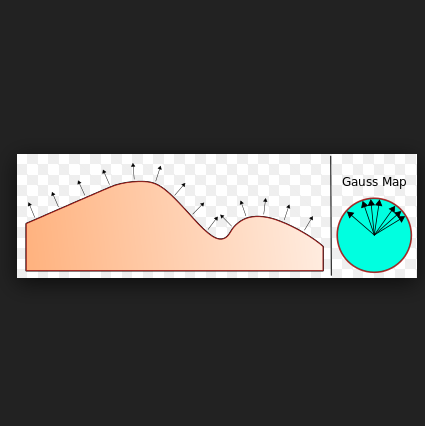
高斯映射是從歐氏空間R3中的一個曲面到單位球面S2的一個映射,以卡爾·弗里德里希·高斯命名。
高斯映射是從歐氏空間R3中的一個曲面到單位球面S2的一個映射,以卡爾·弗里德里希·高斯命名。...
定義高斯球面映射(Gauss spherical map)古典曲面論的高斯映射的一種推廣.設二:M,,}R.}+n是n維光滑流形M"到歐氏空間的等距浸人,二也表示M"的位置向量.利用...
任何這樣鏈環有一個相伴的高斯映射,其度數是環繞數的推廣。 任何標架紐結(framed knot)有一個自環繞數,得自計算紐結C與將曲線C中的點沿著標架向量稍微移動得到...
例如,R中子流形具有平行平均曲率的充分必要條件是它的高斯映射為調和映射.調和映射與全純映射的關係是調和映射理論的又一個重要方面,特別是複流形間的調和映射的全...
這個對應稱為高斯映射。曲面在P點鄰近彎曲程度可用Δб*( 其面積仍用Δб*表示)與Δб的面積比刻畫。主曲率曲面造型上的套用 因為高斯曲率實際反映的是曲面的...
其中轉數是單位切向量關於起點的繞數, 或者等價的高斯映射的次數. 局部不變數曲率和整體拓撲不變數指數的關係是高維黎曼幾何的代表性結果,如高斯-博內定理。 [1]...
恩內佩爾曲面(Enneper's surface)一種重要的極小曲面.在外爾斯特拉斯公式中,令f.=2,}=}=u+iv,D=R,得 該曲面稱為恩內佩爾曲面.它是代數曲面,其高斯映射是...
