非分歧擴張(unramified extension)是一類重要的域擴張。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。
基本介紹
- 中文名:非分歧擴張
- 外文名:unramified extension
- 領域:數學
- 學科:域論
- 性質:一類重要的域擴張
- 相對概念:分歧擴張
概念







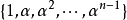
非分歧擴張(unramified extension)是一類重要的域擴張。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。







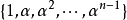
非分歧擴張(unramified extension)是一類重要的域擴張。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常...
全分歧擴張(totally ramified extension)是一類有限賦值域擴張,它是與非分歧擴張相反的概念。賦值域(F,B)的一個有限擴張(K,C),若分歧指數e(C|F)=[K∶F],...
馴分歧擴張(tamely ramified extension)一類包括非分歧擴張在內的代數擴張.設(K,C)是賦值域(F,B)的一個代數擴張,F和I', K和。分別是賦值環B,C的剩餘域和...
分歧指數(ramification index)是在域擴張時,素除子延拓或素理想分解的指數。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴...
不分歧態射(unramified morphism)代數數論中的不分歧擴張的推廣.不分歧態射f:X-}S是概形間的局部有限型態射,使得對每個:ES都有X}=日Spec k,其中k是:的剩餘...
分歧定理(ramification theorem)類域論中判定素理想分歧的定理.若K/k是H的類域,這裡H是k的伊代爾群Jk的含k‘的子群.則k的任一素除子在K非分歧若且唯若Uz....
順分歧(tamely ramified)一種較簡單的分歧情形,包括非分歧情形.設Q為域E的離散素除子,P為其在子域F'上的限制.若剩餘類域擴張E/F可分,且F,的特徵p為零或...
否則就稱為非分歧。如果OK中所有的素理想在L中都是非分歧的,L就稱為K 的一個非分歧擴張。判別式與差積是刻畫分歧的兩個重要概念。令Tr表示有限擴張L到K 的...
希爾伯特類域(Hilbert class field)亦稱最大非分歧阿貝爾擴張。一種重要的類域。最早由希爾伯特(Hilbert,D.)於1898年至1899年猜出,後來發展為系統而一般的類域論...
希爾伯特類域亦稱最大非分歧阿貝爾擴張。一種重要的類域。最早由希爾伯特(Hilbert,D.)於1898年至1899年猜出,後來發展為系統而一般的類域論。數域k的希爾伯特類域...
5.2 非分歧擴張5.3 完全分歧和順分歧5.4 慣性群與分歧群5.5 整體域與局部域5.6 差分5.7 差分與分歧5.8 判別式第六章 整體域:類數與單位...
