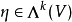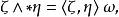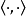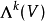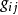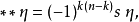基本介紹
- 中文名:霍奇對偶
- 外文名:Hodge dual
- 領域:數學
維數與代數,擴張,k-向量的霍奇星號的正式定義,星運算元的指標記法,k-向量的內積,對偶性,
維數與代數
霍奇星運算元在k-形式空間與 (n-k)-形式空間建立了一個對應。一個k-形式在這個對於下的像稱為這個k-形式的霍奇對偶。k-形式空間的維數是
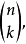
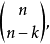
又由二項式係數的對稱性,這兩個維數事實上相等。兩個具有相同維數的形式空間總同構;但不一定有一種自然或典範的方式。但霍奇對偶性利用了向量空間內積和定向,給出了一個特定的同構,因此在代數上這反應了二項式係數的性質。這也在k-形式空間上誘導了一個內積。“自然”定義意味著這個對偶性關係在理論中可起幾何作用。
霍奇對偶在兩個三維空間之間建立起一個同構,一個是V自己,另一個是V中兩個向量的楔積。具體細節參見例子一節。叉積只是三維的特殊性質,但霍奇對偶在所有維數都有效。
擴張
由於一個向量空間上k個變數的交錯線性形式空間自然同構於那個向量空間上的k-向量空間的對偶,霍奇對偶也能對這些空間定義。與線性代數的大部分構造一樣,霍奇對偶可以擴張到一個向量叢。這樣的霍奇對偶特別常見的是在餘切叢的外代數(即流形上的微分形式)上,可用來從外導數構造余微分(codifferential),以及拉普拉斯-德拉姆運算元,它導致了緊黎曼流形上微分形式的霍奇分解。
k-向量的霍奇星號的正式定義
一個定向內積向量空間V上的霍奇星運算元是V的外代數( )上的一個線性運算元,是k-向量子空間(
)上的一個線性運算元,是k-向量子空間(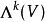 ) 與 (n-k)-向量子空間(
) 與 (n-k)-向量子空間(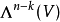 ) 之間的線性映射,這裡
) 之間的線性映射,這裡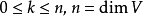 。它具有如下性質,這些性質完全定義了霍奇星運算元:給定一個定向正交基
。它具有如下性質,這些性質完全定義了霍奇星運算元:給定一個定向正交基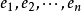 我們有
我們有

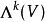
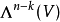
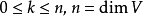
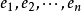
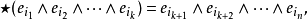
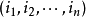
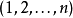
特別是我們有,
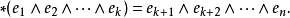
星運算元的指標記法
使用指標記法,霍奇對偶由縮並一個k-形式與n-維完全反對稱列維-奇維塔張量的指標得到。這不同於列維-奇維塔符號有一個額外因子 (detg),這裡g是一個內積(如果g不是正定的,比如洛倫茲流形的切空間,則取行列式的絕對值)。
從而有
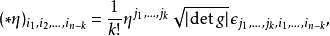
k-向量的內積
霍奇對偶在k-向量空間上誘導了一個內積,即在V的外代數上。給定兩個k-向量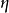 與
與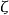 ,有
,有
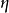
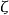
本質上,V的正交基元素的楔積組成了V的外代數的一個正交基。當霍奇星號擴張到流形上,可以證明體積形式能寫做
對偶性
當作用兩次時霍奇星號定義了一個對偶,不考慮符號的話,所得結果是外代數上一個恆等式。給定n-維空間V上一個k-向量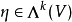 ,我們有
,我們有