零化子(annihilator)起源於零因子的概念.設S是環R的子集,R中一切左乘S中每一個元都等於零的元素的集合,稱為S的左零化子,R中一切右乘S中每一個元都等於零的元素的集合,稱為S的右零化子。
基本介紹
- 中文名:零化子
- 外文名:annihilator
- 所屬學科:數學
- 分類:左零化子、右零化子
定義
定義一

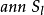










定義二









零化子的性質




1 引理

2 定理

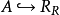




3 定理
4 推論



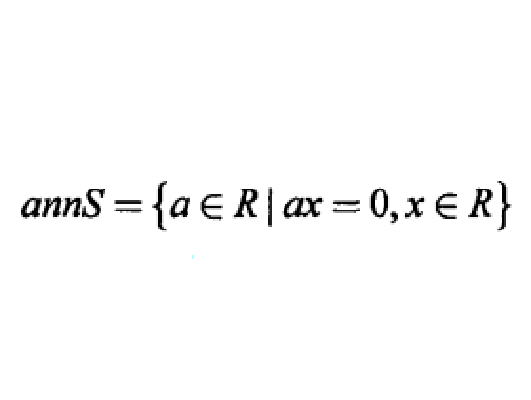
零化子(annihilator)起源於零因子的概念.設S是環R的子集,R中一切左乘S中每一個元都等於零的元素的集合,稱為S的左零化子,R中一切右乘S中每一個元都等於零的元素的集合,稱為S的右零化子。

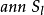

























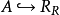







零化子(annihilator)起源於零因子的概念.設S是環R的子集,R中一切左乘S中每一個元都等於零的元素的集合,稱為S的左零化子,R中一切右乘S中每一個元都等於零的...
零化子空間是m維向量空間的與雙線性函式相聯繫的一種子空間。對確定的n維列向量X,滿足f=X'AY=0的m維列向量Y的全體構成m維向量空間P’的子空間,稱為f的零化子...
l零化子(L-annihilator)模的零化子概念的一種套用.設M是格環R上的右格模,A是M的一個非空子集.若r1(A)={xER} }a} }x}=0,對任意的aEA},則稱r} (...
定理4 假定R 是有單位元的半質環如果它又是自內射模,那么R的極大左零化子是極大左理想子環,並且是由R的一個冪等元生成的。定理5 設 那么, 是自內射環當...
稱為α的零化子或零化多項式(annihilator),α的次數最低的首一零化多項式 稱為α的最小零化子。容易證明零化多項式恰為最小零化子的多項式的倍,最小零化子可按以下...
R中所有這種元素作成R的一個左理想,稱為T在R中的左零化子,或R中的一個左零化子。如果環R的任意一組左理想中恆存在極小的左理想,那么環R稱為滿足左極小條件...
凝聚環(coherent ring)是一種與理想的有限生成相關的環類。若環R的任意有限個有限生成左理想的交,以及有限生成左理想的左零化子均為有限生成的,則稱R為左凝聚環...
忠實模(faithful module)是一類重要的模,若M是左A模,把所有與M的乘積為0的A的元的集合記為K,即K={a∈A|aM=0},則K是A的理想,稱為M在A中的零化子。若...
為左R模的直和,則稱左理想集{A; }i EI}是無關的.若環R的左理想組成的任意無關集都是有限的,且R對左零化子有極大條件,則稱R為左哥爾迪環.同樣可定義右...
若R作為分次左R模的分次哥爾迪維數是有限的,且關於分次左零化子有極大條件,則稱R為分次(左)哥爾迪環.若G是有限群且R是分次半素,則R,是哥爾迪環若且唯若...
α-斜Armendariz環中左零化子的一個性質 天水師範學院學報 2008-09 Armendariz環與α-斜Armendariz環 紡織高校基礎科學學報 2010-03 關於M-Armendariz環的註記 天...
