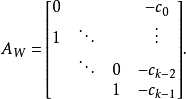
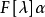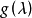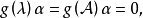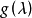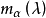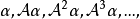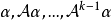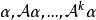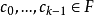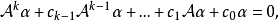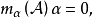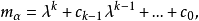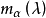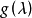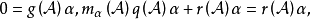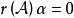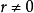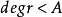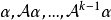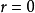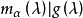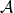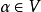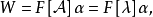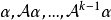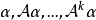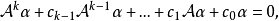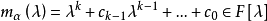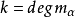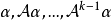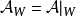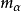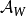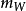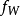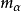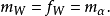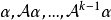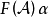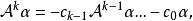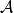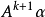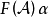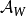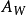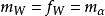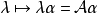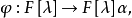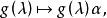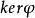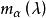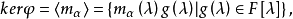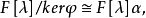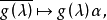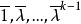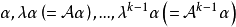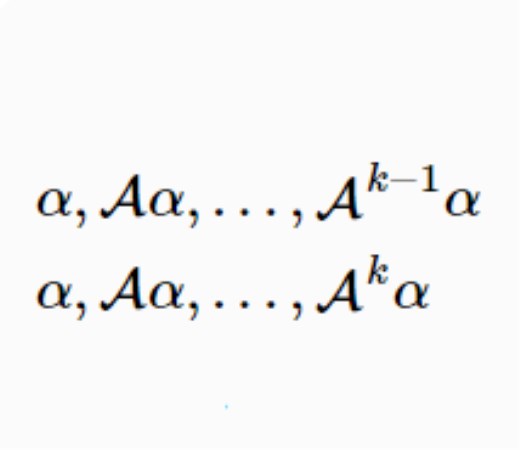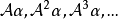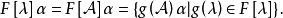循環子空間(cyclic subspace)是一類特殊的子空間,指由一個向量與一個線性變換確定的子空間。設V是域P上的n維線性空間,σ是V上的線性變換,若0≠ξ∈V,則存在k使ξ,σ(ξ),…,σk-1(ξ)線性無關,但ξ,σ(ξ),…,σk(ξ)線性相關,由ξ,σ(ξ),…,σk-1(ξ)生成的子空間L,稱為σ循環子空間,ξ,σ(ξ),…,σk-1(ξ)稱為L的σ循環基。特別地,當L=V時,V稱為循環空間(關於σ的),記為V=L(ξ)σ,而σ稱為循環變換.,V的線性變換σ是循環的充分必要條件是它的最低多項式(也稱最小多項式)的次數為n=dim V,若V=L(ξ)σ,ξ的最低多項式為f(λ)=λn-an-1λn-1-...-a0,則循環變換σ關於基ξ,σ(ξ),…,σk-1(ξ)的矩陣,恰是f(λ)的相伴矩陣。
基本介紹
- 中文名:循環子空間
- 外文名:cyclic subspace
- 所屬學科:數學
- 簡介:由向量與線性變換確定的子空間
基本介紹
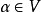
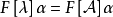
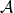
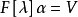
相關概念及性質