基本介紹
- 中文名:忠實模
- 外文名:faithful module
- 所屬學科:數學
- 所屬問題:模與同調代數(模論)
基本介紹,定義,定理,相關概念,即約模,余忠實模,忠實模類,本原環,
基本介紹
定義
假定 是
是 模,如果
模,如果 時
時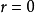 ,即R中任意非零的元不能零化
,即R中任意非零的元不能零化 ,那么
,那么 叫做忠實模。顯然
叫做忠實模。顯然



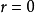




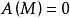

假定 模
模 是既約模,如果R是單環,那么
是既約模,如果R是單環,那么 是忠實模,這是因為
是忠實模,這是因為 是R的理想,如果
是R的理想,如果 ,那么
,那么 ,這與M是既約的假設不合,因此
,這與M是既約的假設不合,因此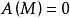 。
。






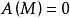
定理
假定 是
是 模,那么
模,那么 是
是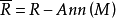 模,並且是忠實模。
模,並且是忠實模。



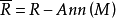
證明: 因為 ,所以
,所以 ,因此
,因此 是
是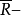 模,再假如
模,再假如 ,即
,即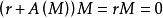 ,那么
,那么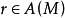 ,所以
,所以 ,於是
,於是 是忠實
是忠實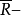 模。證畢。
模。證畢。



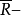

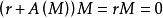
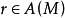


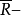
相關概念
即約模
假如N是 模M的子加群,同時又是
模M的子加群,同時又是 模,那么N叫做V的子模。
模,那么N叫做V的子模。 的子模是R的左理想,
的子模是R的左理想, 的子模是R的右理想。同群一樣,模也有商模或差模。只由一個零元組成的
的子模是R的右理想。同群一樣,模也有商模或差模。只由一個零元組成的 模叫做零模,用0表示。任意模M都有0及M自身這兩個子模。只有這兩個平凡子模的模,叫做單模。假如
模叫做零模,用0表示。任意模M都有0及M自身這兩個子模。只有這兩個平凡子模的模,叫做單模。假如 模M是單模,如果
模M是單模,如果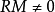 ,那么M叫做既約模,環R的左理想如果又是既約模,叫做R的既約左理想。環R有單位元時它的極小左理想是既約模,因此是R的既約左理想,再假如M是既約模,因為
,那么M叫做既約模,環R的左理想如果又是既約模,叫做R的既約左理想。環R有單位元時它的極小左理想是既約模,因此是R的既約左理想,再假如M是既約模,因為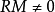 ,所以M=RM。又如果
,所以M=RM。又如果 ,那么
,那么 ,這是因為如果
,這是因為如果 ,設
,設 ={
={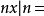 整數或0},那么
整數或0},那么 。於是N是M的子模,今
。於是N是M的子模,今 ,所以N=M,因此RM=0。這與M是既約的假設不合。
,所以N=M,因此RM=0。這與M是既約的假設不合。






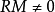
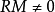




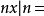


定理 假定R是環,那么 是既約模的必要充分條件是R是體。
是既約模的必要充分條件是R是體。

余忠實模
余忠實模(co-faithful module)是一種特殊的模,是忠實模的對偶概念。設M是A模,若它生成每一個內射A模,則稱M是余忠實模。一個模M是忠實的充分必要條件是,M餘生成每一個投射模;而模AM是余忠實的充分必要條件是,M有限餘生成正則模AA。每一個余忠實的擬內射模一定是內射模。
忠實模類
對每個環A,給定非平凡右A模的一個類 ,定義
,定義 的核為
的核為 中全體A模的零化子的交集
中全體A模的零化子的交集



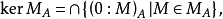




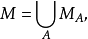
1. 蘊涵
蘊涵 ,其中B是A的理想。
,其中B是A的理想。


2. ,A的理想
,A的理想 蘊涵
蘊涵 。
。



3.若 忠實,則對A的每個非零理想B,
忠實,則對A的每個非零理想B,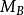 非空。
非空。

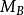
4.若對環A的每個非零理想B,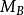 非空,則
非空,則 忠實。
忠實。
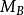

一般模類M確定一個根性質,只要規定環A的根 為模類
為模類 的核,給定一個根性質R,也可構造一個一般模類M,使得對任意環A,均有
的核,給定一個根性質R,也可構造一個一般模類M,使得對任意環A,均有 ,稱這樣的一般模類M為根性質R的模表示或模刻畫。
,稱這樣的一般模類M為根性質R的模表示或模刻畫。



本原環
本原環(primitive ring)是一類重要的環,是研究雅各布森根時引入的,其後被廣泛討論與套用,若環R有一個忠實右(左)R單模(即忠實既約右(左)R模),則稱R為右(左)本原環。通常將右本原環簡稱本原環。一般說來,左本原環未必是本原環,但當R有極小單側理想時,左本原性與本原性一致。任何本原環皆為素環。雅各布森(Jacobson,N.)引入本原環來代替有限條件下的單環,從而得出在沒有有限條件限制下的一般半單環的結構定理,這是環論的重大發展。

