如果函式f在點x連續,則稱x是函式f的連續點;如果函式f在點x不連續,則稱x是函式f的間斷點。
基本介紹
- 中文名:間斷點
- 外文名:point of discontinuity
- 學科:數學
- 領域範圍:函式連續性
- 分類:第一類間斷點和第二類間斷點
定義
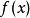
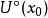
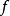
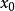
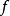
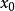
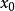
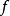
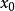
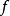
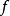
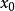
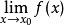
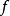
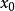
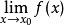
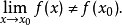
可去間斷點

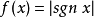

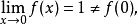

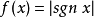


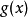
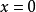
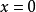
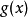


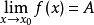
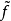


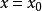
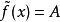
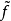


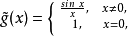
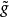

跳躍間斷點

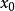






第二類間斷點
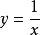
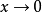

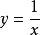
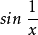


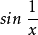

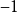

 間斷點分類概括圖
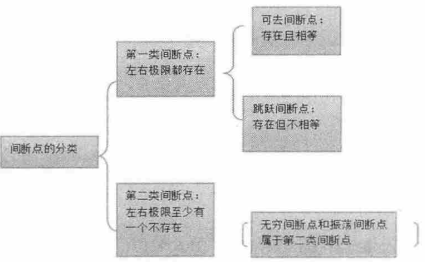
間斷點分類概括圖幾個有間斷點的函式
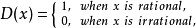
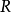

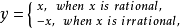
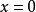
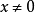
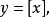






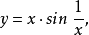




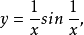

套用
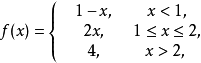




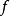
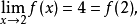
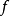
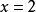
如果函式f在點x連續,則稱x是函式f的連續點;如果函式f在點x不連續,則稱x是函式f的間斷點。
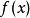
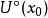
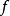
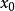
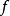
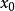
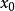
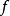
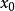
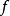
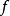
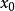
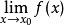
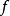
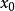
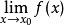
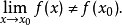

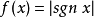

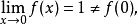

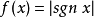


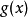
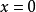
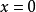
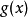


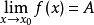
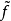


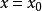
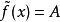
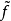


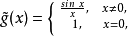
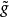


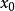






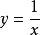
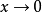

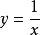
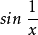


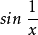

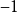

 間斷點分類概括圖
間斷點分類概括圖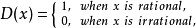
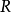

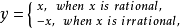
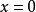
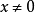
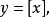






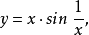




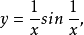

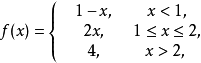




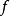
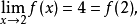
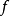
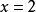
間斷點及其分類第二類間斷點 函式的所有其他形式的間斷點,即使得函式至少有一側極限不存在的那些點,稱為第二類間斷點。例如,函式 當 不存在有限的極限,故 是 的...
間斷點是指:在非連續函式y=f(x)中某點處xo處有中斷現象,那么,xo就稱為函式的不連續點。間斷點可以分為無窮間斷點和非無窮間斷點,在非無窮間斷點中,還分可...
如果x0 是函式 f(x) 的間斷點,且左極限及右極限都存在,則稱 x0 為函式 f(x) 的第一類間斷點(discontinuity point of the first kind)。...
三、間斷點及其分類(111) 練習題3.1 (113) §3.2 連續函式的性質 一、連續函式的局部性質(115) 二、閉區間連續函式的整體性質(116) 三、反函式的連續性(120...
9.理解函式連續性的概念(含左連續與右連續),會判別函式間斷點的類型.10.了解連續函式的性質和初等函式的連續性,理解閉區間上連續函式的性質(有界性、最大值和...
第四章 函式的連續性 l 連續性概念 一 函式在一點的連續性 二 間斷點及其分類 三 區間上的連續函式 2 連續函式的性質 一 連續函式的局部性質 二 閉區間上...
題型16 確定函式的間斷點及其類型題型17 分段函式式中參數的確定(重點)階梯化訓練題基礎能力題綜合提高題參考答案題型演練罄集基礎能力題答案...
2.7 函式的間斷點及其分類 第三章 導數與微分 3.1 導數的概念 3.2 函式的微分法 3.3 微分 3.4 隱函式微分法、參數方程微分法 3.5 高階導數 第...
2.2.6+間斷點的分類與垂直漸近線2.3函式在無窮遠處的極限2.3.1當x→+∞時,函式f(x)的極限及無窮大2.3.2當x→—∞時,函式f(x)的極限及無窮大...
3.5 連續函式的概念 443.5.1 函式的連續與間斷 443.5.2 函式間斷點的類型及其對應的圖形 453.5.3 初等函式的連續性 463.5.4 閉區間上連續函式的性質 47...
8.理解函式連續性的概念(含左連續與右連續),會判別函式間斷點的類型.9.了解連續函式的性質和初等函式的連續性,理解閉區間上連續函式的性質(有界性、最大值和最...
二、 函式的間斷點及其分類53習題1 756第八節連續函式的運算與初等函式的連續性57一、 連續函式的和、差、積、商的連續性 57二、 基本初等函式的連續性57...
4.1 無窮小量及其階 4.2 無窮小的等價代換 4.3 無窮大量 習題1.4 第五節 連續函式 5.1 函式的連續性概念與間斷點的分類 5.2 連續函式的運算性質與...
題型1.1 函式的概念及其特性題型1.2 極限概念與性質題型1.3 函式極限的計算...題型1.7 函式的連續性及間斷點的分類本章總結自測練習題自測練習題答案或提示...
題型1.1 函式、極限的概念及其特性題型1.2 函式極限的計算及其逆問題題型1.3 數列的極限題型1.4 無窮小量的比較題型1.5 函式的連續性及間斷點的分類...
函式連續的概念 函式間斷點的類型 初等函式的連續性 閉區間上連續函式的性質考試要求1. 理解函式的概念,掌握函式的表示法,會建立套用問題的函式關係....
題型九 討論函式的間斷點與間斷點的類型 題型十 閉區間上連續函式命題的證明 第二章 一元函式微分學 考試內容與考試要求 考試內容解析 常考題型及其解法與技巧 題...
第三章 一元函式微分學及其套用一、本章知識結構二、學習基本要求...6. 理解函式連續性的概念,會判別函式間斷點的類型。7. 了......
