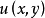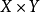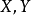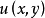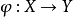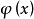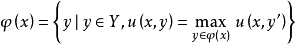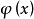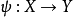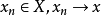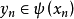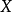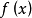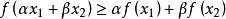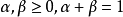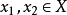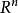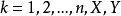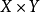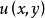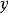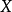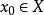連續集值映射(continuous set-valued mapping)是一類特殊的集值映射。設X,Y為拓撲空間,F:X→Y為集值映射,x∈X,若對於F(x)的任意鄰域V,存在x的鄰域U,使得當z∈U時有F(z)⊂V,則稱F在點x是上半連續的,若F在X的任意點都是上半連續的,則稱F為X上的上半連續集值映射。若對於Y的任意開集V,當F(x)∩V≠∅時,存在x的鄰域U,使得當z∈U時有F(z)∩V≠∅,則稱F在點x是下半連續的,若F在X的任意點都是下半連續的,則稱F為X上的下半連續集值映射。上半連續且下半連續的集值映射稱為連續集值映射。這個定義是庫拉托夫斯基(K.Kuratowski)於1932年給出的。
基本介紹
- 中文名:連續集值映射
- 外文名:continuous set-valued mapping
- 所屬學科:數學(一般拓撲學)
- 相關概念:集值映射
- 提出者:庫拉托夫斯基
定義
相關概念
集值映射



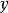





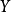

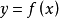



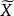


凹函式與凸函式
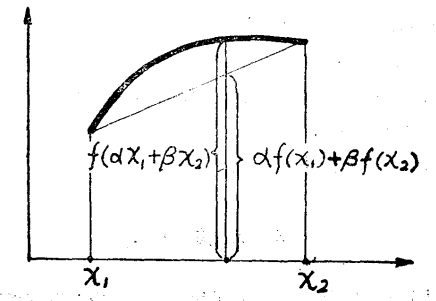 圖1
圖1上半連續
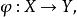
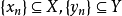
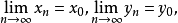

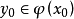


下半連續
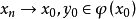
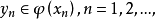


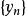
相關性質
線性組合
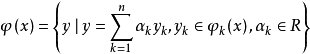
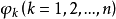

定理1
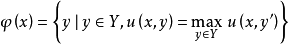

定理2
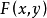
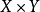

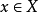
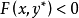
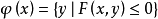
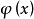
定理3