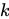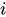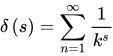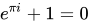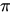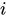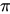猜想提出,猜想內容,歷史研究,接力證明,懸賞求證,莫德爾猜想,谷山豐猜想,證明完成,證明者簡介,社會評價,年表,黎曼猜想、費馬大定理、m理論聯繫在一起,1,從四色定理開始,2,可以構造無窮多個兩兩相連區域,3,圖論與數論聯繫起來,4,篩子與哥德巴赫猜想,5,與費馬大定理聯繫起來,6,與黎曼猜想聯繫起來了,7,一系列數論命題聯合表示m理論,
猜想提出 費馬 大約在1637年左右,法國學者費瑪在閱讀丟番圖(Diophatus)《算術》拉丁文譯本時,曾在第11卷第8命題旁寫道:“將一個立方數分成兩個立方數之和,或一個四次冪分成兩個四次冪之和,或者一般地將一個高於二次的冪分成兩個同次冪之和,這是不可能的。關於此,我確信已發現了一種美妙的證法 ,可惜這裡空白的地方太小,寫不下。”
(拉丁文原文: "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.")
由於費瑪沒有寫下證明,而他的其它猜想對數學貢獻良多,由此激發了許多數學家對這一猜想的興趣。數學家們的有關工作豐富了
數論 的內容,推動了數論的發展。
猜想內容 歷史研究 接力證明 1753年瑞士著名數學家歐拉,在寫給哥德巴赫的信中說,他證明了n=3時的費馬猜想,1770年其證明發表在《代數指南》一書中,方法是“無限下降法”和形如
數系的唯一因子分解定理,這一方法也被後人多次引用。
1816年巴黎科學院把費馬猜想轉化簡化歸結為n是奇素數的情況,認為費馬猜想應該成立,並稱之為費馬大定理(以區別費馬關於同餘的小定理),並為證明者設立大獎和獎章,費馬大定理之謎從此進一步風靡全球。
費馬自己證明了n=4的情形。
十九世紀初法國自學成才的女數學家熱爾曼證明了當n和2n+1都是素數時費馬大定理的反例x,y,z至少有一個是n整倍數。在此基礎上,1825年德國數學家
狄利克雷 和法國數學家勒讓德分別獨立證明費馬大定理在n=5時成立,用的是歐拉所用方法的延伸,但避開了唯一因子分解定理。
1839年,法國數學家拉梅對熱爾曼方法作了進一步改進,並證明了n=7的情形,他的證明使用了跟7本身結合得很緊密的巧妙工具,只是難以推廣到n=11的情形;於是,他又在1847年提出了“分圓整數”法來證明,但沒有成功。
1844年,
庫默爾 提出了“理想數”概念,他證明了:對於所有小於100的素指數n,費馬大定理成立,此一研究告一階段。但對一般情況,在猜想提出的頭二百年內數學家們仍對費馬大定理一籌莫展。
1847年,巴黎科學院上演戲劇性一幕, 當時著名數學家拉梅和柯西先後宣布自己基本證明費馬大定理,拉梅還聲稱證明引用了劉維爾複數系中的唯一因子分解定理,劉維爾則說這一定理源自歐拉和高斯的思想。大數學家都被扯入其中,似乎結論十分可靠。就在此時劉維爾宣讀了德國數學家庫默爾的來信,明確指出證明中的複數系的唯一因子分解定理並不普遍成立,於是拉梅和柯西的證明都是錯的。
大約在1850年前後,
高斯 的學生、德國數學家
庫默爾 看到唯一因子分解是否成立是歐拉、熱爾曼創立的試圖證明費馬大定理的方法關鍵,於是他創立了一種“理想數環”理論,據說這一思想也受其老師高斯啟發,高斯表面上聲稱對費馬大定理不感興趣,實際上對n=7久思不解。學生庫默爾運用獨創的“
理想素數 ”理論,一下子證明了100以內除37、59、67以外的所有奇數費馬大定理都成立,使證明問題取得了第一次重大突破。
庫默爾之後近半個世紀,費馬大定理證明都停滯不前,直到二十世紀前期大數學家
勒貝格 向巴黎科學院提交了一個費馬大定理的證明論稿,由於勒貝格當時的權威聲望,大家都以為這下問題解決了,但經過廣泛傳閱其證明稿件,人們遺憾地發現大數學家的分析證明還是錯的。
懸賞求證 1908年,哥廷根皇家科學協會公布沃爾夫斯凱爾獎:凡在2007年9月13日前解決費馬大定理者將獲得100000馬克獎勵。提供該獎者沃爾夫斯凱爾是德國實業家,年輕時曾為情所困決意在午夜自殺,但在臨自殺前讀到庫默爾論述柯西和拉梅證明費馬定理的錯誤讓他情不自禁地計算到天明,設定自殺時間過了,他也放不下問題的證明,數學讓他重生並後來成為大富豪,1908年這位富豪去世前,遺囑將其一半遺產捐贈設獎,以謝其救命之恩。
從此世界上每年都會有成千上萬人宣稱證明了費馬大定理,但全部都是錯的,一些數學權威機構,不得不預寫證明否定書。
莫德爾猜想 1922年,英國數學家
莫德爾 提出一個著名猜想,人們叫做莫德爾猜想.按其最初形式,這個猜想是說,任一不可約、有理係數的二元多項式,當它的“
虧格 ”大於或等於2時,最多只有有限個解.記這個多項式為f(x,y),猜想便表示:最多存在有限對數偶xi,yi∈
Q ,使得f(xi,yi)=0。後來,人們把猜想擴充到定義在任意數域上的多項式,並且隨著抽象代數幾何的出現,又重新用代數曲線來敘述這個猜想了。
而費馬多項式
沒有奇點,其虧格為
。當
時,費馬多項式滿足猜想的條件。因此,如果莫德爾猜想成立,那么費馬大定理中的方程
本質上最多有有限多個整數解。
二戰後隨著計算機的出現,大量的計算已不再成為問題。藉助計算機的幫助,數學家們對500以內,然後在1000以內,再是10000以內的值證明了費馬大定理,到80年代,這個範圍提高到25000,然後是400萬以內。
1983年,德國數學家
法爾廷斯 證明了莫德爾猜想,從而翻開了費馬大定理研究的新篇章.法爾廷斯也因此獲得1986年
菲爾茲獎 。
谷山豐猜想 1955年,日本數學家
谷山豐 首先猜測橢圓曲線與另一類數學家們了解更多的曲線——模曲線之間存在著某種聯繫;谷山的猜測後經韋依和志村五郎進一步精確化而形成了所謂“谷山—志村猜想”,這個猜想說明了:有理數域上的橢圓曲線都是模曲線。這個很抽象的猜想使一些學者搞不明白,但它又使“費馬大定理”的證明向前邁進了一步。
1958年英國數學家Birch和Swinnerton--Dyer構造了橢圓曲線E的L(E,s)函式,他們對該函式在s=1處的零點與橢圓曲線E上的有理點關係給出了一個簡稱BSD猜想。
1984年,德國數學家弗雷在德國小城奧伯沃爾法赫的一次數論研討會上宣稱:假如費馬大定理不成立,則由費馬方程可構造一個橢圓曲線,它不可被模形式化(一個
命題 :假定“費馬大定理”不成立,即存在一組非零整數
使得
,那么用這
組數 構造出的形如
乘以
的橢圓曲線,不可能是模曲線。),也就是說谷山—志村猜想將不成立。但弗雷構造的所謂“弗雷曲線”不可模形式化也說不清具體證明細節,因此也只是猜想,被稱為“弗雷命題”,弗雷命題如得證,費馬大定理就與谷山—志村猜想等價。
1986年美國加州大學伯克利分校的肯·里貝特教授,為了證明弗雷命題已經奮鬥了十八個月,曾親耳聽到弗雷當年演講的里貝特深信自己能證明弗雷命題,但久攻未克,這年夏天哈佛大學教授巴里·梅袓爾來伯克利訪問並參加國際數學家大會,有一次里貝特與他一起喝咖啡,便研討起弗雷命題,梅袓爾的一個提醒讓里貝特恍然大悟,里貝特隨即完成了弗雷命題的證明,並當即在這屆國際數學家大會內外傳開。世界數學界為之興奮。
證明完成 1986年,英國數學家
安德魯·懷爾斯 聽到里貝特證明弗雷命題後,感到攻克費馬大定理到了最後攻關階段,並且這剛好是他的研究領域,他開始放棄所有其它活動,精心梳理有關領域的基本理論,為此準備了一年半時間把橢圓曲線與模形式通過伽羅瓦表示方法“排隊”。接下來的要將兩種“排隊”序列對應配對,這一步他兩年無進展。此時他讀博時學的岩澤理論一度取得實效,到1991年他之前的導師科茨告訴他有位叫弗萊切的學生用蘇聯數學家科利瓦金的方法研究橢圓曲線,這一方法使其工作有重大進展。
安德魯·懷爾斯 1993年6月在劍橋牛頓學院要舉行一個名為“L函式和算術”的學術會議,組織者之一正是懷爾斯的博士導師科茨,於是在1993年6月21日到23日懷爾斯被特許在該學術會上以“模形式、橢圓曲線與伽羅瓦表示”為題,分三次作了演講。聽完演講人們意識到谷山—志村猜想已經證明。由此把法爾廷斯證明的莫德爾猜想、肯·里貝特證明的弗雷命題和懷爾斯證明的谷山—志村猜想聯合起來就可說明費馬大定理成立。其實這三個猜想每一個都非常困難,問題是懷爾斯的最後證明,他變為完成費馬大定理證明的最後一棒。
1993年6月23日從劍橋牛頓學院傳出費馬大定理被證明之後,世界媒體鋪天蓋地般報導了該喜訊。
但此刻數學界反倒十分冷靜,明確指出論證還需仔細審核,因為歷史上曾多少次宣布證明但後來被查證錯誤。懷爾斯的證明被分為6個部分分別由6人審查,其中由凱茲負責的第三部分查出關於歐拉系的構造有嚴重缺陷,使科利瓦金—弗萊切方法不能對它適用,懷爾斯對此無能為力,1993年12月懷爾斯公開承認證明有問題,但表示很快會補正。一時間懷爾斯的證明被認為是歷史上拉梅、柯西、勒貝格、里貝特(里貝特也曾稱證明了谷山—志村猜想)錯誤證明的又一例子。1994年1月懷爾斯邀請劍橋大學講師理察·泰勒到普林斯頓幫他完善科利瓦金—弗萊切方法解決問題,但整整8個月過去,問題沒有解決。泰勒準備再過一個月後回劍橋,然後懷爾斯正式公布手稿,承認證明失敗,1994年9月19日懷爾斯想自己證明失敗原因該怎么寫,回顧自己是先用岩澤理論未能突破而後用科利瓦金—弗萊切方法,又對該法一類特殊歐拉系出了問題,這樣一想,突然又想到何不再用岩澤理論結合科利瓦金—弗萊切方法試試?問題解法就是這樣,懷爾斯絕處逢生,修補了漏洞。1994年10月25日11點4分11秒,懷爾斯通過他以前的學生、美國俄亥俄州立大學教授卡爾·魯賓向世界數學界傳送了費馬大定理的完整證明郵件,包括一篇長文“模形橢圓曲線和費馬大定理”,作者安德魯·懷爾斯。另一篇短文“某些赫克代數的環理論性質”作者理察·泰勒和安德魯·懷爾斯。至此費馬大定理得證。
1995年,他們把證明過程發表在《
數學年刊 》(Annals of Mathematics)第141卷上,證明過程包括兩篇文章,共130頁,占滿了全卷,題目分別為Modular elliptic curves and Fermat’s Last Theorem(模形橢圓曲線和費馬大定理)以及Ring-theoretic properties of certain Hecke algebras(某些赫克代數的環理論性質)。
證明者簡介 安德魯·懷爾斯(Andrew Wiles),英國著名數學家、牛津大學教授、美國科學院外籍院士。現在任教於英國
牛津大學 。
1996年3月,懷爾斯獲得沃爾夫獎(Wolf Prize)和5萬美金。
1997年6月27日,懷爾斯獲得沃爾夫斯凱爾10萬馬克懸賞大獎,就在哥廷根皇家科學協會規定期只剩下10年的時候沃爾夫斯凱爾當年遺願終於實現。
1998年第23屆
國際數學家大會 在柏林舉行,國際數學聯合會還史無前例地頒給懷爾斯
菲爾茲特別獎, 一個特殊製作的
菲爾茲獎 銀質獎章。
1999年,他榮獲首屆克萊數學研究獎 (Clay Research Award)。
2000年,懷爾斯被授勳為爵士。
2005年,懷爾斯又榮獲有“東方諾貝爾獎”之稱的
邵逸夫數學科學獎 (Shaw Prize),獎金100萬美金。
2005年8月29日,安德魯·懷爾斯第一次踏上中國的土地,這甚至是他第一次來到亞洲。北京大學數學院院長張繼平、副院長劉化榮,中科院院士田剛、張恭慶、姜伯駒、丁偉岳、文蘭等陪同他參觀中國。
2016年3月15日,挪威自然科學與文學院宣布將2016年阿貝爾獎 (Abel Prize) 授予牛津大學的安德魯·懷爾斯 (Andrew Wiles) 教授,獎金約600萬挪威克朗(約465萬元人民幣),表彰他令人震驚的費馬大定理證明。
其他榮譽還包括羅夫·肖克獎 (Rolf Schock Prize)、奧斯特洛斯基獎 (Ostrowski Prize)、英國皇家學會皇家獎章 (Royal Medal of the Royal Society)、美國國家科學院數學獎 (U.S. National Academy of Science’s Award in Mathematics) 等。
社會評價 史上最精彩的一個數學謎題。
證明費馬大定理的過程是一部數學史。
費馬大定理起源於三百多年前,挑戰人類3個世紀,多次震驚全世界,耗盡人類眾多最傑出大腦的精力,也讓千千萬萬業餘者痴迷。
這是“20世紀最輝煌的數學成就”。(中科院院士、北大數學院教授
姜伯駒 ,評價安德魯·懷爾斯對費馬大定理的證明)
年表 1637年,費瑪在書本空白處提出費馬猜想。
1770年,歐拉證明n=3時定理成立
1823年,勒讓德證明n=5時定理成立。
1832年,狄利克雷試圖證明n=7失敗,但證明 n=14時定理成立。
1839年,拉梅證明n=7時定理成立。
1850年,庫默爾證明2<n<100時除37、59、67三數外定理成立。
1955年,范迪維爾以電腦計算證明了 2<n<4002時定理成立。
1976年,瓦格斯塔夫以電腦計算證明 2<n<125000時定理成立。
1985年,羅瑟以電腦計算證明2<n<41000000時定理成立。
1987年,格朗維爾以電腦計算證明了 2<n<101800000時定理成立。
1995年,懷爾斯證明 n>2時定理成立。
黎曼猜想、費馬大定理、m理論聯繫在一起 當我們用
霍奇猜想 的方法製造幾何拓撲超級結構時:一種歧管。這個歧管的整體就是費馬大定理,計算這個結構局部就要用
黎曼猜想 。
1,從四色定理開始 法蘭西斯·古德里於1852年提出的猜想,只需要四種顏色為地圖著色。這是因為他發現在平面上或者球面上,只能有4個區域兩兩相連,英國數學家德摩根證明了平面上不存在5個區域兩兩相連。
1974年德國的林格和美國的楊斯證明了在曲面上染色定理,例如,在一個汽車輪胎形狀的環面需要7種顏色,因為可以構造7個兩兩相連的區域,6種顏色肯定不夠的;在有兩個洞的雙環面需要8種顏色,因為可以構造8個兩兩相連的區域,7種顏色肯定不夠的;...參見
N色定理 .。
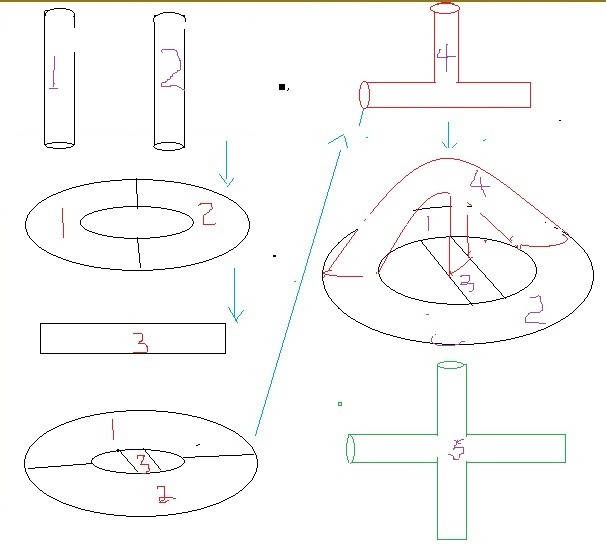
2,可以構造無窮多個兩兩相連區域 現在有兩根管子,一個記為1,一個記為2,它們代表兩個區域。我們假定所有的管子都是可以隨意拉伸和彎曲的。把兩根管子端端相連,就是一個汽車輪胎一樣的環,它有兩個區域,我們再用一根直管子記為3,安在這個環的中間,一頭連著區域1,一頭連著區域2,現在它是有兩個洞的雙環了,有三個區域兩兩相連。
把歧管兩兩相連之間給定距離可以等價轉換成為
貨郎擔問題 (p=np問題)。
3,圖論與數論聯繫起來 數學家和物理學家把上面這個叫做岐管。
在數論中,最重要的元素就是素數,歐幾里得證明了有無窮多個素數,並且它們有一個特點就是兩兩互素。無窮多個兩兩互素的素數與無窮多個兩兩相連區域一一對應。
圖論與數論聯繫起來了。
我們把這個圖的岐管倒過來,就像一個網子,籃球網子。籃球網子是把籃球往裡面投。
4,篩子與哥德巴赫猜想 公元前300年古希臘有一個數學家叫做埃拉特斯特尼,他把這個網子當成篩子,把自然數往裡面扔,他說凡是合數通過篩子以後就會從網子裡面篩掉,留下的是素數,這個就是著名的埃拉特斯特尼篩法。
上面這個岐管
篩子 是把偶數往裡面扔,
哥德巴赫猜想 說,大於4的偶數一個也不會漏出篩子,除了6=3+3以外,其他偶數都是可以在不同的素數區域被攔截。例如8會在區域2也就是素數3和素數5(第三個區域)被攔截;偶數10會在素數3和素數7的兩個區域之間被攔截;....。總之,無窮多個偶數都逃不脫這個網子,沒有一個偶數可以漏到外面去。
數論 與
圖論 已經融合一起了,這個想法叫做
朗蘭茲綱領 。
5,與費馬大定理聯繫起來 這個還不算神奇,這個岐管的內部空間我們記為
,外部空間記為
,它有很多洞,可以有無窮多個洞,可以有無窮多個空間維度
,宇宙內外整體記為1,就是說
,這個叫做費馬曲線.。
費馬大定理與哥德巴赫猜想聯繫起來了。
6,與黎曼猜想聯繫起來了 數學家考慮的是怎樣計算這個岐管上的區域或者計算區域上面的一個點。如果岐管上某一個區域
,在
上的一個點是
,因為這個岐管有無窮多個維度,或者很多維度,要定位這個點,就要考慮它的管壁——實部,還有考慮它的內外空間位置——虛部。 所以,這個點
,
。
是虛數,α表示實部,實部是
,因為這個多維宇宙等於1,岐管屬於實部,實部上的點當然是1/2。這個正是黎曼函式
,
隨意在岐管上畫出一條線,都需要黎曼猜想計算。計算虛部需要歐拉公式。 物理學裡,真空是能量的“零點”。
黎曼猜想與物理學和費馬大定理聯繫起來了。
現在大家看到了黎曼猜想直接滲透到幾何拓撲。
虛部怎么樣計算呢?
虛部怎么計算呢?岐管內部看成一個圓管,虛部是什麼?它至少應該有管道內或者管道外中的一個參數。假設管道截面是一個圓,管道內的截面圓依然是二維平面,在岐管上的一個點,就是一個圓。大家知道歐拉公式嗎?
,
以
開始,以相對速度
,走了
時間(虛時間),再加1,回到原點(解析延拓)。(右下圖)
虛時間是為了對應時間起點(大爆炸)而定義的一個概念。在虛時間這個概念體系里,在比三維更高的維度空間,時間並不是一條直線,而是一個閉合的圓,沒有起始也沒有終結,宇宙的起點如果源自大爆炸,那在此之前的時間將無法定義。因此,為了解決奇點之前時間應該如何,我們引用到了複數的概念。
歐拉公式:
(3)式看似荒唐,其實是虛時間真實的時空穿越,現在的人“
”與過去的人“
” 在同一時空相遇。也可以理解為兩個光量子糾纏,只要知道一個就可以知道另外一個。
7,一系列數論命題聯合表示m理論 數學家製造代數或者數論的目的是為幾何服務,即便最簡單的整數也是為離散幾何服務。幾何拓撲進展是創造代數或者數論的源泉,創造一個新代數結構必須為它找到幾何新結構。
物理學家認為,宇宙是10維空間或者11維空間,或者26維空間等5個版本。還有物理學家認為有無窮多個維度的空間。他們管這個理論叫做弦理論或者M理論,是把廣義相對論與量子理論結合一起的終極理論,霍金說是最後的理論。
在弦/m理論的11維空間裡, 幾何體的拓撲性質同粒子緊密相關。例如,這種粒子幾何體有幾個洞,決定著粒子世代的數目,在這些捲縮維度的空間裡所採取的幾何構型決定著弦或者膜能夠有什麼樣的震動模式,從而決定著各種粒子的質量、自旋、以及電荷等各種相互作用的耦合常數。
原來,不僅僅自旋和同位旋等內部變數和內部空間都出自這些多維空間的幾何學,而且粒子的電荷質量等性質,無一不是從這裡產生出來的,不僅僅如此,甚至我們生活本身也通過三維空間和一維時間都是從類似的幾何體的構造中生長出來的。 我們生活在高維宇宙的一小片中,大到銀河宇宙,小至原子夸克,都是弦線構成的。
 費馬
費馬






 安德魯·懷爾斯
安德魯·懷爾斯