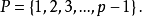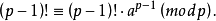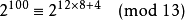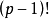發展簡史
皮埃爾·德·費馬於1636年發現了這個定理。在一封1640年10月18日的信中他第一次使用了上面的書寫方式。在他的信中費馬還提出a是一個
素數的要求,但是這個要求實際上是不必要的。
1736年,歐拉出版了一本名為“一些與素數有關的定理的證明”(
拉丁文:Theorematum Quorundam ad Numeros PRIMOS Spectantium Demonstratio)”的論文中第一次提出
證明,但從
萊布尼茨未發表的手稿中發現他在1683年以前已經得到幾乎是相同的證明。
有些學家獨立製作相關的假說(有時也被錯誤地稱為中國的假說),當成立時,p是
素數。這是費馬小定理的一個特殊情況。然而,這一假說的前設是錯的:例如,341 ,而341= 11×31是一個
偽素數。所有的偽素數都是此假說的
反例。
如
上所述,中國猜測僅有一半是正確的。符合中國猜測但不是素數的數被稱為偽素數。
更極端的反例是卡麥可數: 假設a與561互質,則 a
560被561除都餘1。這樣的數被稱為卡麥可數數,561是最小的卡麥可數。Korselt在1899年就給出了卡麥可數的等價定義,但直到1910年才由
卡麥可(Robert Daniel Carmichael)發現第一個卡麥可數:561。1994年William Alford、Andrew Granville及Carl Pomerance證明了卡麥可數有無窮多個。
驗證推導
引理1.
若a,b,c為任意3個整數,m為正整數,且(m,c)=1,則當a·c≡b·c(mod m)時,有a≡b(mod m)。
證明:a·c≡b·c(mod m)可得ac–bc≡0(mod m)可得(a-b)·c≡0(mod m)。因為(m,c)=1即m,c互質,c可以約去,a– b≡0(mod m)可得a≡b(mod m)。
引理2.
設m是一個
整數且m>1,b是一個
整數且(m,b)=1。如果a[1],a[2],a[3],a[4],…a[m]是模m的一個完全剩餘系,則b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也構成模m的一個完全剩餘系。
證明:若存在2個整數b·a[i]和b·a[j]同餘即b·a[i]≡b·a[j](mod m)..(i>=1 && j>=1),根據引理1則有a[i]≡a[j](mod m)。根據完全剩餘系的
定義可知這是不可能的,因此不存在2個
整數b·a[i]和b·a[j]同餘。
所以b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]構成模m的一個完全剩餘系。
這樣就證明了費馬小定理。
定理意義
套用
故餘數為3。
證明對於任意整數a而言,
恆為2730的倍數。13減1為12,12的正因數有1, 2, 3, 4, 6, 12,分別加1,為2, 3, 4, 5, 7, 13,其中2, 3, 5, 7, 13為質數,根據定理,
為2的倍數、為3的倍數、為5的倍數、為7的倍數、為13的倍數,即2*3*5*7*13=2730的倍數。
Python程式碼
>>> n =221
>>>a = 38
>>>pow(a ,n -1,n)
1
"""221 may be a prime number."""
import random
def isprime(n,k=128):
if n<2:
return False
for _ in range(k):
a = random.randrange(1,n)
if pow(a,n-1,n)!=1:
return False
return True