費馬偽素數

費馬偽素數（英語：Fermat pseudoprime）是指滿足費馬小定理的偽素數，也是最重要的一類偽素數。

基本介紹

• 中文名：費馬偽素數
• 外文名：Fermat pseudoprime
• 領域：數學
• 本質：一類偽素數
• 條件：滿足費馬小定理

定義

其定義是：對自然數和一個與其互素的自然數a，如果整除a- 1，則稱是一個以a為底的費馬偽素數或者關於a的費馬偽素數。最小的費馬偽素數是341（=11×31，關於2）。如果關於任何與其互素的數都是費馬偽素數，則稱是絕對偽素數（或卡麥可數，來自找到第一個絕對偽素數的數學家羅伯特·丹尼·卡麥可）。最小的絕對偽素數是561。

有人已經證明了費馬偽素數的個數是無窮的。有一位數學家如此評論：“對於素數，費馬小定理肯定是正確的；但他沒說在合數中就不正確。”事實上，費馬小定理給出的是關於素數判定的必要非充分條件。

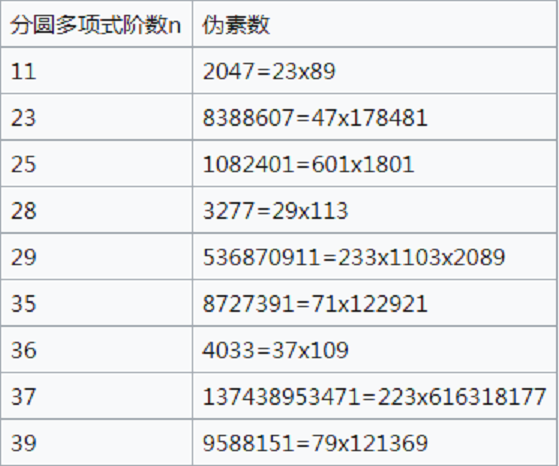
另外，若: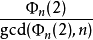不是素數(如下表中的情況)，則它就一定是偽素數。 這些當中包含了所有的費馬合數(當n=2)，梅森合數(當n=p)及瓦格斯塔夫合數(當n=2p)

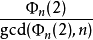
費馬偽素數年表

1819年，薩魯斯（Sarrus）發現第一個偽素數341

1903年，馬洛（Malo）證明：若n為偽素數，則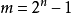也是一個偽素數，從而肯定了偽素數的個數是無窮的。

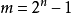
1950年，發現第一個偶偽素數。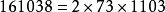

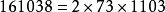
1951年，皮格（Beeger）證明了存在無限多個偶偽素數。

以2為底的前50個費馬偽素數

（OEIS中的數列A001567）

n		n		n		n		n
1	341 = 11 · 31	11	2821= 7 · 13 · 31	21	8481 = 3 · 11 · 257	31	15709 = 23 · 683	41	30121 = 7 · 13 · 331
2	561= 3 · 11 · 17	12	3277 = 29 · 113	22	8911= 7 · 19 · 67	32	15841= 7 · 31 · 73	42	30889 = 17 · 23 · 79
3	645 = 3 · 5 · 43	13	4033 = 37 · 109	23	10261 = 31 · 331	33	16705 = 5 · 13 · 257	43	31417 = 89 · 353
4	1105= 5 · 13 · 17	14	4369 = 17 · 257	24	10585= 5 · 29 · 73	34	18705 = 3 · 5 · 29 · 43	44	31609 = 73 · 433
5	1387 = 19 · 73	15	4371 = 3 · 31 · 47	25	11305 = 5 · 7 · 17 · 19	35	18721 = 97 · 193	45	31621 = 103 · 307
6	1729= 7 · 13 · 19	16	4681 = 31 · 151	26	12801 = 3 · 17 · 251	36	19951 = 71 · 281	46	33153 = 3 · 43 · 257
7	1905 = 3 · 5 · 127	17	5461 = 43 · 127	27	13741 = 7 · 13 · 151	37	23001 = 3 · 11 · 17 · 41	47	34945 = 5 · 29 · 241
8	2047 = 23 · 89	18	6601= 7 · 23 · 41	28	13747 = 59 · 233	38	23377 = 97 · 241	48	35333 = 89 · 397
9	2465= 5 · 17 · 29	19	7957 = 73 · 109	29	13981 = 11 · 31 · 41	39	25761 = 3 · 31 · 277	49	39865 = 5 · 7 · 17 · 67
10	2701 = 37 · 73	20	8321 = 53 · 157	30	14491 = 43 · 337	40	29341= 13 · 37 · 61	50	41041= 7 · 11 · 13 · 41

以任意整數為底的最小費馬偽素數

（OEIS中的數列A007535）

a	最小的偽素數	a	最小的偽素數	a	最小的偽素數	a	最小的偽素數
1	4 = 2^2	51	65 = 5 · 13	101	175 = 5^2 · 7	151	175 = 5^2 · 7
2	341 = 11 · 31	52	85 = 5 · 17	102	133 = 7 · 19	152	153 = 3^2 · 17
3	91 = 7 · 13	53	65 = 5 · 13	103	133 = 7 · 19	153	209 = 11 · 19
4	15 = 3 · 5	54	55 = 5 · 11	104	105 = 3 · 5 · 7	154	155 = 5 · 31
5	124 = 2^2 · 31	55	63 = 3^2 · 7	105	451 = 11 · 41	155	231 = 3 · 7 · 11
6	35 = 5 · 7	56	57 = 3 · 19	106	133 = 7 · 19	156	217 = 7 · 31
7	25 = 5^2	57	65 = 5 · 13	107	133 = 7 · 19	157	186 = 2 · 3 · 31
8	9 = 3^2	58	133 = 7 · 19	108	341 = 11 · 31	158	159 = 3 · 53
9	28 = 2^2 · 7	59	87 = 3 · 29	109	117 = 3^2 · 13	159	247 = 13 · 19
10	33 = 3 · 11	60	341 = 11 · 31	110	111 = 3 · 37	160	161 = 7 · 23
11	15 = 3 · 5	61	91 = 7 · 13	111	190 = 2 · 5 · 19	161	190=2 · 5 · 19
12	65 = 5 · 13	62	63 = 3^2 · 7	112	121 = 11^2	162	481 = 13 · 37
13	21 = 3 · 7	63	341 = 11 · 31	113	133 = 7 · 19	163	186 = 2 · 3 · 31
14	15 = 3 · 5	64	65 = 5 · 13	114	115 = 5 · 23	164	165 = 3 · 5 · 11
15	341 = 11 · 31	65	112 = 2· 7	115	133 = 7 · 19	165	172 = 2^2 · 43
16	51 = 3 · 17	66	91 = 7 · 13	116	117 = 3^2 · 13	166	301 = 7 · 43
17	45 = 3^2 · 5	67	85 = 5 · 17	117	145 = 5 · 29	167	231 = 3 · 7 · 11
18	25 = 5^2	68	69 = 3 · 23	118	119 = 7 · 17	168	169 = 13^2
19	45 = 3^2 · 5	69	85 = 5 · 17	119	177 = 3 · 59	169	231 = 3 · 7 · 11
20	21 = 3 · 7	70	169 = 13^2	120	121 = 11^2	170	171 = 3^2 · 19
21	55 = 5 · 11	71	105 = 3 · 5 · 7	121	133 = 7 · 19	171	215 = 5 · 43
22	69 = 3 · 23	72	85 = 5 · 17	122	123 = 3 · 41	172	247 = 13 · 19
23	33 = 3 · 11	73	111 = 3 · 37	123	217 = 7 · 31	173	205 = 5 · 41
24	25 = 5^2	74	75 = 3 · 5^2	124	125 = 3^3	174	175 = 5^2 · 7
25	28 = 2^2 · 7	75	91 = 7 · 13	125	133 = 7 · 19	175	319 = 11 · 19
26	27 = 3^3	76	77 = 7 · 11	126	247 = 13 · 19	176	177 = 3 · 59
27	65 = 5 · 13	77	247 = 13 · 19	127	153 = 3^2 · 17	177	196 = 2^2 · 7^2
28	45 = 3^2 · 5	78	341 = 11 · 31	128	129 = 3 · 43	178	247 = 13 · 19
29	35 = 5 · 7	79	91 = 7 · 13	129	217 = 7 · 31	179	185 = 5 · 37
30	49 = 7^2	80	81 = 3	130	217 = 7 · 31	180	217 = 7 · 31
31	49 = 7^2	81	85 = 5 · 17	131	143 = 11 · 13	181	195 = 3 · 5 · 13
32	33 = 3 · 11	82	91 = 7 · 13	132	133 = 7 · 19	182	183 = 3 · 61
33	85 = 5 · 17	83	105 = 3 · 5 · 7	133	145 = 5 · 29	183	221 = 13 · 17
34	35 = 5 · 7	84	85 = 5 · 17	134	135 = 3^3 · 5	184	185 = 5 · 37
35	51 = 3 · 17	85	129 = 3 · 43	135	221 = 13 · 17	185	217 = 7 · 31
36	91 = 7 · 13	86	87 = 3 · 29	136	265 = 5 · 53	186	187 = 11 · 17
37	45 = 3^2 · 5	87	91 = 7 · 13	137	148 = 2^2 · 37	187	217 = 7 · 31
38	39 = 3 · 13	88	91 = 7 · 13	138	259 = 7 · 37	188	189 = 3^3 · 7
39	95 = 5 · 19	89	99 = 3^2 · 11	139	161 = 7 · 23	189	235 = 5 · 47
40	91 = 7 · 13	90	91 = 7 · 13	140	141 = 3 · 47	190	231 = 3 · 7 · 11
41	105 = 3 · 5 · 7	91	115 = 5 · 23	141	355 = 5 · 71	191	217 = 7 · 31
42	205 = 5 · 41	92	93 = 3 · 31	142	143 = 11 · 13	192	217 = 7 · 31
43	77 = 7 · 11	93	301 = 7 · 43	143	213 = 3 · 71	193	276 = 2^2 · 3 · 23
44	45 = 3^2 · 5	94	95 = 5 · 19	144	145 = 5 · 29	194	195 = 3 · 5 · 13
45	76 = 2^2 · 19	95	141 = 3 · 47	145	153 = 3^2 · 17	195	259 = 7 · 37
46	133 = 7 · 19	96	133 = 7 · 19	146	147 = 3 · 7^2	196	205 = 5 · 41
47	65 = 5 · 13	97	105 = 3 · 5 · 7	147	169 = 13^2	197	231 = 3 · 7 · 11
48	49 = 7^2	98	99 = 3^2 · 11	148	231 = 3 · 7 · 11	198	247 = 13 · 19
49	66 = 2 · 3 · 11	99	145 = 5 · 29	149	175 = 5^2 · 7	199	225 = 3^2 · 5^2
50	51 = 3 · 17	100	153 = 3^2 · 17	150	169 = 13^2	200	201 = 3 · 67