歐拉偽素數（英語：Euler pseudoprime）是偽素數的一種。
基本介紹
- 中文名：歐拉偽素數
- 外文名：Euler pseudoprime
定義,示例,
定義
對於奇合數n以及與其互素的自然數a，如果
成立，則稱n為關於a的歐拉偽素數。歐拉偽素數是費馬偽素數的推廣，所有歐拉偽素數同時也是費馬偽素數。
與費馬偽素數類似，歐拉偽素數的定義也是源於費馬小定理。該定理表明，對於素數p以及整數a，有
。對大於2的素數p，p可以表示為2q + 1 ，其中q為整數。於是
成立。再進一步化簡為
。通過因式分解，得到
，即
。
上式可以用作機率素性檢驗，其可靠性是費馬素性檢驗的兩倍。不過無法基於歐拉偽素數對素數進行確定性檢驗，因為存在絕對歐拉偽素數，即其關於所有與其互素的數都是歐拉偽素數。絕對歐拉偽素數是卡麥可數（即絕對費馬偽素數）的子集。最小的絕對歐拉偽素數為1729 = 7×13×19。
示例
關於n的歐拉偽素數如圖所示
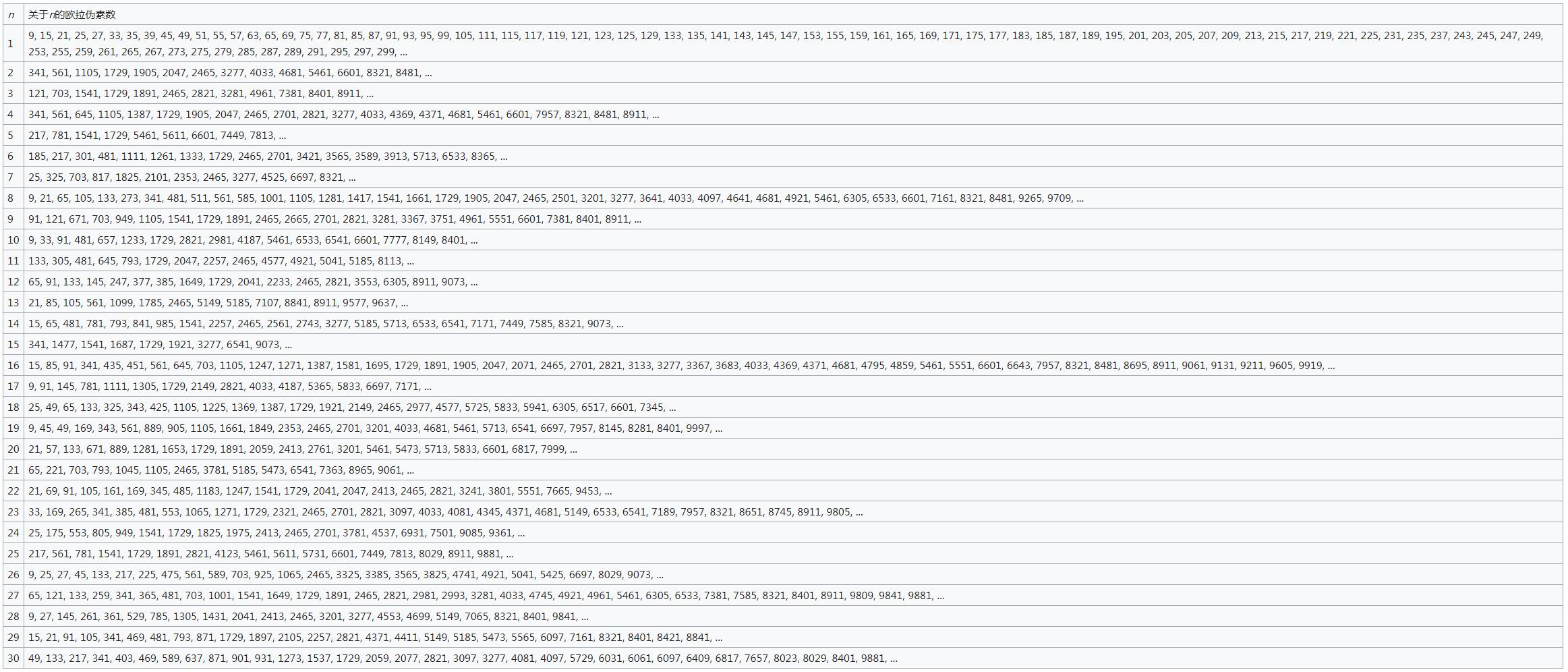關於n的歐拉偽素數