費馬素性檢驗

費馬素性檢驗是一種素數判定法則，利用隨機化算法判斷一個數是合數還是可能是素數。

基本介紹

  • 中文名：費馬素性檢驗
  • 屬性：素數判定法則
  • 作用：判斷數是合數還是可能是素數
  • 方法：利用隨機化算法
  • 學科：計算機
  • 領域：計算機
概念,算法以及運行時間,缺點,套用,參見,

概念

根據費馬小定理：如果p是素數，
，那么
如果我們想知道n是否是素數，我們在中間選取a，看看上面等式是否成立。如果對於數值a等式不成立，那么n是合數。如果有很多的a能夠使等式成立，那么我們可以說n可能是素數，或者偽素數。
在我們檢驗過程中，有可能我們選取的a都能讓等式成立，然而n卻是合數。這時等式
被稱為Fermat liar。如果我們選取滿足下面等式的a
那么a也就是對於n的合數判定的Fermat witness。
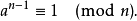
a
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
最小的n值
4
341
91
15
4
35
6
9
4
9
10
65
4
15
14
15
4
25
6
21
4
21
22
25
4
9
26
9
4
49

算法以及運行時間

整個算法可以寫成是下面兩大部：
  • 輸入：n需要檢驗的數；k：參數之一來決定檢驗需要進行的次數。
  • 輸出：當n是合數時，否則可能是素數：
  • 重複k次：
    在[1,n− 1]範圍內隨機選取a
  • 如果amodn≠ 1那么返回合數
返回可能是素數
若使用模指數運算的快速算法，這個算法的運行時間是O(k×logn)，這裡k是一個隨機的a需要檢驗的次數，n是我們想要檢驗的數。

缺點

眾所周知，對於卡米歇爾數n，全部的a都會令gcd(a,n)=1，我們稱之為費馬騙子數（Fermat liars）。儘管卡米歇爾數很是稀有，但是卻足夠令費馬素性檢驗無法像如米勒-拉賓和Solovay-Strassen的素性檢驗般，成為被經常實際套用的素性檢驗。
一般的，如果n不是卡米歇爾數，那么至少一半的
是費馬證人數（Fermat witnesses）。在這裡，令a為費馬證人數、a1,a2, ...,as為費馬騙子數。那么
所有的a×aifori= 1, 2, ...,s都是費馬證人數。

套用

加密程式PGP在算法當中用到了這個素性檢驗方法。

參見

相關詞條

熱門詞條

聯絡我們