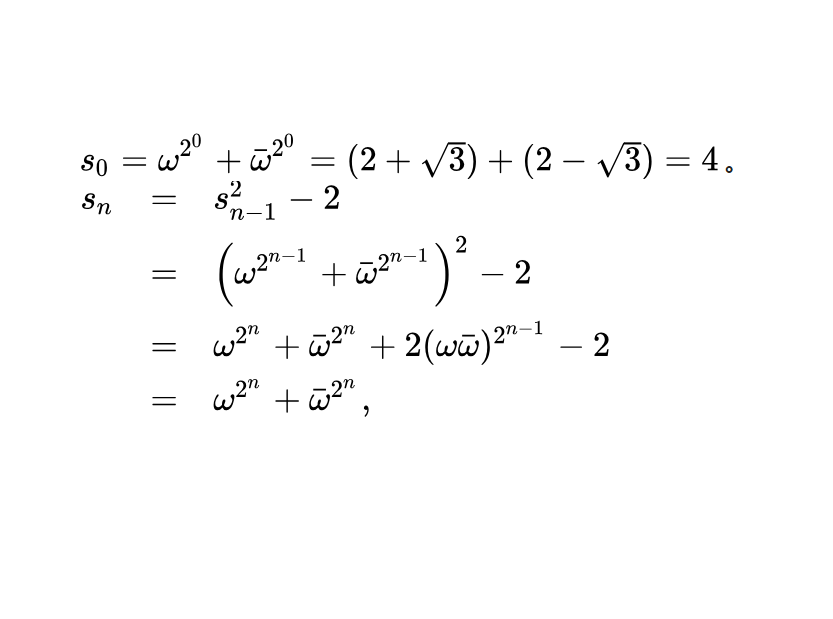盧卡斯-萊默檢驗法

數學中，盧卡斯-萊默檢驗法（英語：Lucas–Lehmer primality test）是檢驗梅森數的素性檢驗，是由愛德華·盧卡斯於1878年完善，德里克·亨利·萊默（英語：Derrick Henry Lehmer）隨後於1930年代將其改進。

基本介紹

• 中文名：盧卡斯-萊默檢驗法
• 外文名：Lucas–Lehmer primality test
• 套用：檢驗梅森數的素性檢驗
• 完善：愛德華·盧卡斯於1878年
• 改進：德里克·亨利·萊默隨後於1930年代

方法

令梅森數M_p=2^p-1作為檢驗對象,定義數列{L_n}:L₀=4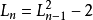，,n>0.這個數列的開始幾項是4,14,194,37634,1416317954……那么M_p是質數若且唯若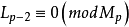.否則M_p是合數。s_p−2模M_p的餘數叫做M_p的盧卡斯－萊默餘數。

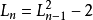
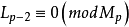
例子

假設我們想驗證M₃ = 7是素數。我們從s=4開始，並更新3−2=1次，把所有的得數模7：

• s ← ((4 × 4) − 2) mod 7 = 0
  

由於我們最終得到了一個能被7整除的s，因此M₃是素數。

另一方面，M₁₁ = 2047 = 23 × 89就不是素數。我們仍然從s=4開始，並更新11−2=9次，把所有的得數模2047：

• s ← ((4 × 4) − 2) mod 2047 = 14
  
• s ← ((14 × 14) − 2) mod 2047 = 194
  
• s ← ((194 × 194) − 2) mod 2047 = 788
  
• s ← ((788 × 788) − 2) mod 2047 = 701
  
• s ← ((701 × 701) − 2) mod 2047 = 119
  
• s ← ((119 × 119) − 2) mod 2047 = 1877
  
• s ← ((1877 × 1877) − 2) mod 2047 = 240
  
• s ← ((240 × 240) − 2) mod 2047 = 282
  
• s ← ((282 × 282) − 2) mod 2047 = 1736
  

由於s最終仍未能被2047整除，因此M₁₁=2047不是素數。但是，我們從這個檢驗法仍然無法知道2047的因子，只知道它的盧卡斯-萊默餘數1736。