裴蜀定理

在數論中，裴蜀定理是一個關於最大公約數（或最大公約式）的定理，裴蜀定理得名於法國數學家艾蒂安·裴蜀。

裴蜀定理說明了對任何整數 a、b和它們的最大公約數 d ，關於未知數 x 和 y 的線性丟番圖方程（稱為裴蜀等式）。

基本介紹

• 中文名：裴蜀定理
• 外文名：Bézout's identity
• 別稱：貝祖定理
• 提出者：艾蒂安·裴蜀
• 套用學科： 數學 信息學
• 適用領域範圍：數論

簡介

裴蜀定理（或貝祖定理，Bézout's identity）得名於法國數學家艾蒂安·裴蜀，說明了對任何整數a、b和它們的最大公約數d，關於未知數x和y的線性不定方程（稱為裴蜀等式）：若a,b是整數,且gcd(a,b)=d，那么對於任意的整數x,y,ax+by都一定是d的倍數，特別地，一定存在整數x,y，使ax+by=d成立。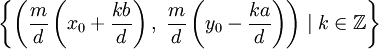

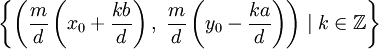
它的一個重要推論是：a,b互質的充要條件是存在整數x,y使ax+by=1.

證明

證法一：

設 則 。由整除的性質， ，有d|(ax+by)。設s為ax+by最小正值，首先有d|s,

令 ，, 可見 也為 的線性組合。由於 為 線性組合的最小正值, ，可知 。則 ,同理 ,則 ，因此可得 ，命題得證。

證法二：

⑴若b=0，則（a,b)=a.這時定理顯然成立。

⑵若a,b不等於0.

記d = (a, b), 對ax + by = d，兩邊同時除以d，可得(a1)x + (b1)y = 1，其中(a1,b1) = 1。
轉證(a1)x + (b1)y = 1。由帶餘除法：
① (a1) = (q1)(b1) + (r1), 其中0 < r1 < b1
② (b1) = (q2)(r1) + (r2), 其中0 < r2 < r1
③ (r1) = (q3)(r2) + (r3), 其中0 < r3 < r2
.....
④ (rn-4) = (qn-2)(rn-3) + (rn-2)
⑤ (rn-3) = (qn-1)(rn-2) + (rn-1)
⑥ (rn-2) = (qn)(rn-1) + (rn)
⑦ (rn-1) = (qn+1)(rn) + 1
故，由⑦和⑥推出(rn-2)An-2 + (rn-1)Bn-1 = 1
再結合⑤推出(rn-3)An-3 + (rn-2)Bn-2 = 1
再結合④推出(rn-4)An-4 + (rn-3)Bn-3 = 1
.....
再結合③推出(r1)A1 + (r2)B2 = 1
再結合②推出(b1)A0 + (r1)B0 = 1
再結合①推出(a1)x + (b1)y = 1
證畢。

n個整數間的裴蜀定理

設a1,a2,a3......an為n個整數，d是它們的最大公約數，那么存在整數x1......xn使得x1*a1+x2*a2+...xn*an=d。

特別來說，如果a1...an互質（不是兩兩互質），那么存在整數x1......xn使得x1*a1+x2*a2+...xn*an=1。證法類似兩個數的情況。

任意主理想環上的情況

裴蜀可以推廣到任意的主理想環上。設環A是主理想環，a和b 為環中元素，d是它們的一個最大公約元，那么存在環中元素x和y使得：

ax + by = d

這是因為在主理想環中，a和b的最大公約元被定義為理想aA + bA的生成元。

定理

在數論中，裴蜀定理是一個關於最大公約數（或最大公約式）的定理。裴蜀定理得名於法國數學家艾蒂安·裴蜀，說明了對任何整數a、b和它們的最大公約數d，關於未知數x和y的線性丟番圖方程（稱為裴蜀等式）：

ax + by = m

有解若且唯若m是d的倍數。裴蜀等式有解時必然有無窮多個整數解，每組解x、y都稱為裴蜀數，可用輾轉相除法求得。

例如，12和42的最大公因子是6，則方程12x + 42y = 6有解。事實上有（-3）×12 + 1×42 = 6及4×12 + (-1）×42 = 6。

特別來說，方程 ax + by = 1 有解若且唯若整數a和b互素。

裴蜀等式也可以用來給最大公約數定義：d其實就是最小的可以寫成ax + by形式的正整數。這個定義的本質是整環中“理想”的概念。因此對於多項式整環也有相應的裴蜀定理。

歷史

歷史上首先證明關於整數的裴蜀定理的並不是裴蜀，而是17世紀初的法國數學家克勞德-加斯帕·巴歇·德·梅齊里亞克（Claude-Gaspard Bachet de Méziriac）。他在於1624年發表的著作《有關整數的令人快樂與愜意的問題集》（Problèmes plaisans et délectables qui se font par les nombres）第二版中給出了問題的描述和證明[1]。

然而，裴蜀推廣了梅齊里亞克的結論，特別是探討了多項式中的裴蜀等式，並給出了相應的定理和證明[2]。

整數中的裴蜀定理

對任意兩個整數a、b設d是它們的最大公約數。那么關於未知數x和y的線性丟番圖方程（稱為裴蜀等式）：

ax + by = m

有整數解（x,y）若且唯若m是d的倍數。裴蜀等式有解時必然有無窮多個解。

裴蜀定理參見

理想 （環論）

歐幾里德整環

歐幾里德引理

主理想環

整除

裴蜀定理-參考來源

^ 原版的網上版本（法文）

^ 證明的網上版本（法文）

閔嗣鶴、嚴士健，初等數論，高等教育出版社，2003。

唐忠明，抽象代數基礎，高等教育出版社，2006。

Algebraic curves ，2008版，Chapter5.3。

推廣

以上定理可推廣到n個，n≥2

如1st IMO 1959第1題：證明對任意自然數n，（21n+4）/（14n+3）為既約分數。證明：很容易看出3（14n+3）-2（21n+4）=1，由裴蜀定理，21n+4與14n+3互質，故（21n+4）/（14n+3）為既約分數。Q.E.D.

另如：5x+4y+3z可表示全部整數.因為3，4，5互質，所以5x+4y+3z可以等於1，則必定可以等於其他任意整數。